Catalanova ploskev
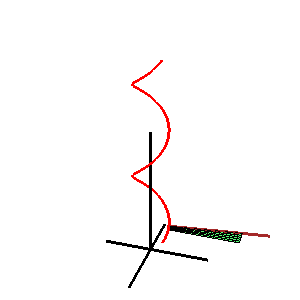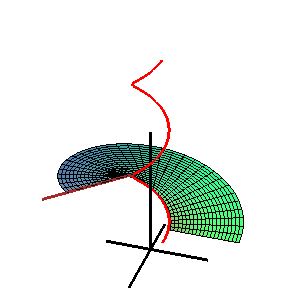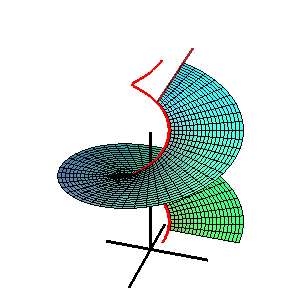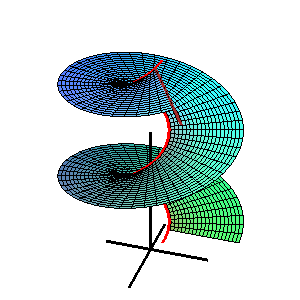
Catalanova ploskev je premonosna ploskev. Smeri, ki omogočajo nastanek ploskve, so vzporedne fiksni ravnini.
Vektorska enačba Catalanove ploskve je
- r = s(u) + v L(u)
kjer je
- r = s(u) prostorska krivulja
- L(u) je enotski vektor v smeri premonosne ploskve. Vsi vektorji L(u) so vzporedni isti ravnini, ki je ravnina direktrise ploskve.
Parametrična enačba Catalanove ploskve je
- .
Če vse premonosne premice Catalanove ploskve sekajo fiksno premico, se ploskev imenuje konoida.
Imenuje se po belgijskem matematiku Eugènu Charlesu Catalanu (1814 - 1894)