Tristrana ortobikupola

Tristrana ortobikupola
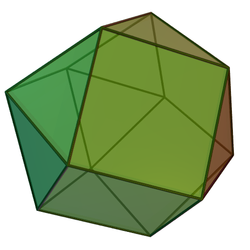
Vrsta	Johnsonovo telo J26-J27-J28
Stranske ploskve	2+6 trikotnikov 6 kvadratov
Oglišča	12
Robovi	24
Konfiguracija oglišča	6(32.42) 6(3.4.3.4)
Grupa simetrije	D3h
Dualni polieder	trapezo rombski dodekaeder
Lastnosti	konveksna
mreža telesa

Tristrana ortobikupola je eno izmed Johnsonovih teles (J₂₇). Kot že ime nakazuje, jo dobimo tako, da pritrdimo dve tristrani kupoli (J₃) na njihove osnovne ploskve. Ima enako število kvadratov in trikotnikov na vsakem oglišču. Ni pa ogliščno tranzitivna. Imenujemo jo tudi antikubooktaeder.

Tristrana ortobikupola je prva v neskončni množici ortobikupol.

Tristrana ortobikupola nas močno spominja na kubooktaeder, ki je znan kot tristrana girobikupola v imenovanju Johnsonovih teles. Razlika je samo v tem, da sta dve tristrani kupoli, ki tvorita tristrano ortobikupolo, povezani tako, da so pari stranic dotikajo. Kubooktaeder je povezan tako, da se trikotniki in kvadrati dotikajo ter obratno. Za dano ortobikupolo nam vrtenje za 60º ene izmed kupol pred združevanjem da kubooktaeder. Zaredi tega je tudi drugo ime za ortobikulo antikubooktaeder.

Podaljšano tristrano ortobikupolo (J₃₅), ki jo dobimo s podaljševanjem tega telesa, ima poseben in drugačen odnos z rombikubooktaederom.

Dualno telo tristrane ortobikupole se imenuje trapezo-rombski dodekaeder. Ta ima 6 rombskih in 6 trapezoidnih stranskih ploskev. Podoben je rombskemu dodekaedru. Oba sta poliedra, ki zapolnjujeta prostor.

Prostornina in površina

Naslednja izraza za prostornino (V) in površino (P) so uporabni za vse vrste stranskih ploskev, ki so pravilne in imajo dolžino roba a

$V=\frac{5\sqrt{2}}{3}{a}^3\approx 2,35702...a^3$

$P=2(3+\sqrt{3})a^2\approx 9,4641...a^2$

Polmer očrtane sfere tristrane ortobikupole je enak dolžini roba (C=a).

Zunanje povezave

• Johnsonovo telo na MathWorld Predloga:Ikona en
• Tristrana ortobikupola na MathWorld Predloga:Ikona en
• Tristrana ortobikupola na Bulatov.org Predloga:Ikona en
• Tristrana ortobikupola na Polyhedra.org Predloga:Webarchive Predloga:Ikona en