Dirichletova funkcija eta

Barvna predstavitev Dirichletove funkcije $\eta (s)$ v kompleksni ravnini. Barva točke $s$ odkriva vrednost funkcije $\eta (s)$. Temnejše barve označujejo vrednosti blizu nič, odtenek pa argument vrednosti. Ustvarjena je s tiskalniško knjižnico matplotlib z različico metode domenskega barvanja.

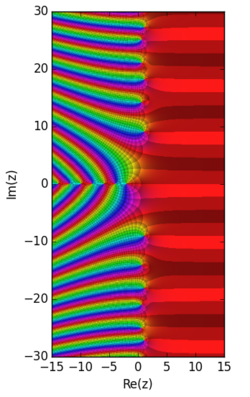
Dirichletova funkcija eta (običajna označba $\eta (s)$) je v matematiki in še posebej v analitični teoriji števil specialna funkcija definirana kot Dirichletova vrsta, ki konvergira za vsako kompleksno število z realnim delom večjim od 0:

$\eta (s)=\sum _{n=1}^{\mathrm{\infty }}\frac{(-1{)}^{n-1}}{n^s}=\frac{1}{1^s}-\frac{1}{2^s}+\frac{1}{3^s}-\frac{1}{4^s}+\cdots ,(\mathrm{\Re }(s)>0).$

Imenuje se po nemškem matematiku Petru Gustavu Lejeuneu Dirichletu. Ta Dirichletova vrsta je alternirajoča vsota, ki odgovarja razvoju Riemannove funkcije ζ(s) v Dirichletovo vrsto. Zaradi tega je Dirichletova funkcija η znana tudi kot alternirajoča funkcija zeta, označena tudi kot ${\zeta }_{*}(s)$. Velja naslednja preprosta zveza:

$\eta (s)=(1-\frac{2}{2^s})\zeta (s)=(1-\frac{1}{2^{s-1}})\zeta (s)=(1-2^{1-s})\zeta (s).$

Čeprav razvoj Dirichletove funkcije η v Dirichletovo vrsto konvergira le za vsako kompleksno število s z realnim delom večjim od 0, njegova Abelova vsota obstaja za poljubno kompleksno število. Zaradi tega se lahko Dirichletova funkcija η definira kot cela funkcija. Zgornja zveza tako kaže, da je Riemannova funkcija ζ meromorfna z enostavnim polom v točki s = 1 in morda v polih v drugih ničlah s faktorjem $1-2^{1-s}$.

Enakovredno se lahko definira:

$\eta (s)=\frac{1}{\mathrm{\Gamma }(s)}\underset{0}{\overset{\mathrm{\infty }}{\int }}\frac{x^{s-1}}{e^x+1}\mathrm{d}x,$

kjer je Γ(s) funkcija Γ. Tako določena funkcija je definirana tudi v območju pozitivnega realnega dela. To da Dirichletovo funkcijo η kot Mellinova transformacija.

Hardy je dal preprost dokaz funkcijske enačbe za Dirichletovo funkcijo η:

$\eta (-s)=2\frac{1-2^{-s-1}}{1-2^{-s}}{\pi }^{-s-1}s\sin \left(\frac{\pi s}{2}\right)\mathrm{\Gamma }(s)\eta (s+1).$

Od tod neposredno izhaja tudi funkcijska enačba za Riemannovo funkcijo ζ, kakor tudi drug način za razširitev definicije Dirichletove funkcije η na celotno kompleksno ravnino.

Eulerjev produkt za Dirichletovo funkcijo η

Pomembnost Dirichletove funkcije η v teoriji števil je podobno kot Riemannove funkcije ζ v njeni povezanosti s praštevili, ki jo za $\mathrm{\Re }(s)>1$ podaja neskončni Eulerjev produkt:

$\eta (s)=(1-\frac{1}{2^{s-1}})\prod _{p\in \mathbb{P}}\frac{1}{1-\frac{1}{p^s}}=(1-\frac{1}{2^{s-1}})\frac{1}{(1-\frac{1}{2^s})(1-\frac{1}{3^s})(1-\frac{1}{5^s})\cdots }.$

Ničle Dirichletove funkcije η

Ničle Dirichletove funkcije η vsebujejo vse ničle Riemannove funkcije ζ: za neskončno mnogo negativnih sodih celih števil (realne enako oddaljene enostavne (trivialne) ničle); neskončno mnogo ničel vzdolž kritične premice, od katerih je znano, da ni nobena mnogokratna, in več kot 40 %, za katere se je dokazalo, da so enostavne, in domnevne ničle na kritičnem traku in ne tudi na kritični premici. Če zadnje obstajajo, morajo ležati na ogliščih pravokotnikov simetrično okrog osi x in kritične premice, njihova multiplikativnost pa ni znana. Poleg tega faktor $1-2^{1-s}$ doda neskončno mnogo kompleksni enostavnih ničel, ki ležijo na enako oddaljenih točkah na premici $\mathrm{\Re }(s)=1$, v $s_n=1+2n\pi i/\ln 2$, kjer je n neničelno celo število.

Po Riemannovi domnevi naj bi ničle Dirichletove funkcije η ležale simetrično glede na realno os na dveh vzporednih premicah $\mathrm{\Re }(s)=1/2,\mathrm{\Re }(s)=1$, in na pravokotnem poltraku, ki ga tvori negativna realna os.

Landauov problem z ζ(s) = η(s)/0 in rešitve

V enačbi η(s) = (1−2^1−s) ζ(s) se »pol funkcije ζ(s) v točki s = 1 izniči z ničlo drugega faktorja,« tako, da vrednost η(1) ni niti neskončna niti enaka 0. Vendar mora v enačbi:

$\zeta (s)=\frac{\eta (s)}{1-2^{1-s}},$

funkcija η biti enaka 0 v vseh točkah $s_n=1+n\frac{2\pi }{\ln 2}i,n\ne 0,n\in Z$, kjer je števec enak 0, če je Riemannova funkcija ζ tam analitična in končna. Na problem dokazovanja tega brez vnaprejšnje definicije Riemannove funkcije ζ je opozoril Landau v svoji razpravi o teoriji ševil iz leta 1909: »Ali je vrsta η različna od 0 ali ne v točkah $s_n\ne 1$, oziroma ali so to poli ali ne, tukaj ni takoj razvidno.«

Prvo rešitev Landauovega problema je skoraj 40 let kasneje objavil Widder v svoji knjigi The Laplace Transform. Uporabil je naslednje praštevilo 3 namesto 2 za definicijo Dirichletove vrste, ki je podobna funkciji η. Tako definirana funkcija se imenuje funkcija $\lambda$ in je definirana za $\mathrm{\Re }(s)>0$ z nekaterimi ničlami tudi na $\mathrm{\Re }(s)=1$, vendar te niso enake kot tiste pri funkciji η. Predloga:Hidden begin

$\begin{array}{c}\lambda (s)=(1-\frac{3}{3^s})\zeta (s)=(1+\frac{1}{2^s})-\frac{2}{3^s}+(\frac{1}{4^s}+\frac{1}{5^s})-\frac{2}{6^s}+\dots \end{array}$

Če je $s$ realen in strogo pozitiven, vrsta konvergira, ker se predznak skupaj zloženih členov zaporedoma spreminja, njihova absolutna vrednost pa pada proti 0. Po izreku o enakomerni konvergenci Dirichletove vrste, ki ga je prvi dokazal Cahen leta 1894, je funkcija $\lambda (s)$ potem analitična za $\mathrm{\Re }(s)>0$, območje, ki vključuje premico $Re(s)=1$. Sedaj se lahko ustrezno definira kjer števci niso enaki 0:

$\zeta (s)=\frac{\eta (s)}{1-\frac{2}{2^s}},$

ali:

$\zeta (s)=\frac{\lambda (s)}{1-\frac{3}{3^s}}.$

Ker je $\frac{\ln 3}{\ln 2}$ iracionalno število, števci v obeh definicijah istočasno niso enaki 0 razen za $s=1$, in je tako funkcija $\zeta (s)$ dobro definirana in anaalitična za $\mathrm{\Re }(s)>0$ razen v točki $s=1$. Končno se posredno dobi, da je $\eta (s_n)=0$ kadar je $s_n\ne 1$:

$\eta (s_n)=(1-\frac{2}{2^{s_n}})\zeta (s_n)=\frac{1-\frac{2}{2^{s_n}}}{1-\frac{3}{3^{s_n}}}\lambda (s_n)=0.$

Elementarni in od $\zeta$ neodvisni dokaz za ničelnost funkcije η v $s_n\ne 1$ je objavil Sondow leta 2003. Izraža vrednost funkcije η kot limito posebnih Riemannovih vsot povezanih z integralom, za katerega se ve, da je enak 0, z zvezo med delnimi vsotami Dirichletove vrste, ki določajo funkciji η in ζ za $\mathrm{\Re }(s)>1$.

Predloga:Hidden begin Z enostavno algebro na končnih vsotah se lahko za poljubni kompleksni s zapiše:

${\eta }_{2n}(s)=\sum _{k=1}^{2n}\frac{(-1{)}^{k-1}}{k^s}=1-\frac{1}{2^s}+\frac{1}{3^s}-\frac{1}{4^s}+\dots +\frac{(-1{)}^{2n-1}}{{(2n)}^s}=1+\frac{1}{2^s}+\frac{1}{3^s}+\frac{1}{4^s}+\dots +\frac{1}{{(2n)}^s}-2(\frac{1}{2^s}+\frac{1}{4^s}+\dots +\frac{1}{{(2n)}^s})$

$=(1-\frac{2}{2^s}){\zeta }_{2n}(s)+\frac{2}{2^s}(\frac{1}{{(n+1)}^s}+\dots +\frac{1}{{(2n)}^s})=(1-\frac{2}{2^s}){\zeta }_{2n}(s)+\frac{2n}{{(2n)}^s}\frac{1}{n}(\frac{1}{{(1+1/n)}^s}+\dots +\frac{1}{{(1+n/n)}^s}).$

Če je sedaj $s=1+it$ in $2^s=2$, je faktor, ki množi funkcijo ${\zeta }_{2n}(s)$, enak 0, in velja:

${\eta }_{2n}(s)=\frac{1}{n^{it}}{R}_n(\frac{1}{{(1+x)}^s},0,1),$

kjer Rn(f(x),a,b) označuje posebno Riemannovo vsoto, ki aproksimira integral funkcije f(x) čez [a,b]. Za t = 0, oziroma s = 1, velja:

$\eta (1)=\underset{n\to \mathrm{\infty }}{\lim }{\eta }_{2n}(1)=\underset{n\to \mathrm{\infty }}{\lim }{R}_n(\frac{1}{1+x},0,1)=\underset{0}{\overset{1}{\int }}\frac{\mathrm{d}x}{1+x}=\ln 2\ne 0.$

Drugače, če je $t\ne 0$, potem velja $|n^{1-s}|=|n^{-it}|=1$, od koder sledi:

$|\eta (s)|=\underset{n\to \mathrm{\infty }}{\lim }|{\eta }_{2n}(s)|=\underset{n\to \mathrm{\infty }}{\lim }|R_n(\frac{1}{{(1+x)}^s},0,1)|=|\underset{0}{\overset{1}{\int }}\frac{\mathrm{d}x}{{(1+x)}^s}|=|\frac{2^{1-s}-1}{1-s}|=|\frac{1-1}{-it}|=0.$

Če se privzame $\eta (s_n)=0$ za vsako točko $s_n\ne 1$, kjer je $2^{s_n}=2$, se lahko sedaj definira funkcija $\zeta (s_n)$ z zveznosjo kot sledi:

$\zeta (s_n)=\underset{s\to s_n}{\lim }\frac{\eta (s)}{1-\frac{2}{2^s}}=\underset{s\to s_n}{\lim }\frac{\eta (s)-\eta (s_n)}{\frac{2}{2^{s_n}}-\frac{2}{2^s}}=\underset{s\to s_n}{\lim }\frac{\eta (s)-\eta (s_n)}{s-s_n}\frac{s-s_n}{\frac{2}{2^{s_n}}-\frac{2}{2^s}}=\frac{{\eta }^{\prime }(s_n)}{\ln 2}.$

Navidezna singularnost funkcije ζ v $s_n\ne 1$ je sedaj odstranjena, dokazano pa je, da je funkcija ζ analitična povsod v $\mathrm{\Re }(s)>0$, razen v točki $s=1$, kjer je:

$\underset{s\to 1}{\lim }(s-1)\zeta (s)=\underset{s\to 1}{\lim }\frac{\eta (s)}{\frac{1-2^{1-s}}{s-1}}=\frac{\eta (1)}{\ln 2}=1.$

Integralski izrazi

Navede se lahko več integralskih formul, ki vsebujejo funkcijo η. Prva sledi iz spremembe spremenljivke integralske reprezentacije funkcije Γ, kar da Mellinovo transformacijo, ki se lahko izrazi na različne načine kot dvojni inegral.. To velja za $\mathrm{\Re }(s)>0$:

$\begin{array}{cc}\mathrm{\Gamma }(s)\eta (s)& =\underset{0}{\overset{\mathrm{\infty }}{\int }}\frac{x^{s-1}}{e^x+1}\mathrm{d}x=\underset{0}{\overset{\mathrm{\infty }}{\int }}\underset{0}{\overset{x}{\int }}\frac{x^{s-2}}{e^x+1}\mathrm{d}y\mathrm{d}x\\ & =\underset{0}{\overset{\mathrm{\infty }}{\int }}\underset{0}{\overset{\mathrm{\infty }}{\int }}\frac{(t+r{)}^{s-2}}{e^{t+r}+1}\mathrm{d}r\mathrm{d}t=\underset{0}{\overset{1}{\int }}\underset{0}{\overset{1}{\int }}\frac{(-\ln (xy){)}^{s-2}}{1+xy}\mathrm{d}x\mathrm{d}y.\end{array}$

Cauchy-Schlömilchova transformacija se lahko uporabi za dokaz te druge reprezentacije, veljavne za $\mathrm{\Re }(s)>-1$. Integracija po delih prvega integrala zgoraj v tem razdelku da drugo izpeljavo:

$2^{1-s}\mathrm{\Gamma }(s+1)\eta (s)=2\underset{0}{\overset{\mathrm{\infty }}{\int }}\frac{x^{2s+1}}{{\cosh }^2(x^2)}\mathrm{d}x=\underset{0}{\overset{\mathrm{\infty }}{\int }}\frac{t^s}{{\cosh }^2(t)}\mathrm{d}t.$

Naslednja formula po Lindelöfu iz leta 1905 velja za celotno kompleksno ravnino, kjer je glavna vrednost vzeta za logaritem implicitno v eksponentu:

$\eta (s)=\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\frac{(1/2+it{)}^{-s}}{e^{\pi t}+e^{-\pi t}}\mathrm{d}t.$

To odgovarja Jensenovi formuli iz leta 1895 za celo funkcijo $(s-1)\zeta (s)$, veljavno na celotni kompleksni ravnini, kar je tudi dokazal Lindelöf:

$(s-1)\zeta (s)=2\pi \underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\frac{(1/2+it{)}^{1-s}}{(e^{\pi t}+e^{-\pi t}{)}^2}\mathrm{d}t.$

Jensen je zapisal: »Ta formula, enkratna po svoji preprostosti, se lahko dokaže enostavno s pomočjo Cauchyjevega izreka, tako pomembnega za seštevanje vsot.« Podobno s pretvorbo integracijske poti na konturne integrale se lahko dobi druge formule za funkcijo η, kot je na primer naslednja posplošitev, veljavna za $0<c<1$ in vse $s$ :

$\eta (s)=\frac{1}{2}\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}\frac{(c+it{)}^{-s}}{\sin (\pi (c+it))}\mathrm{d}t.$

Ničle negativne realne osi se izničijo, ko gre $c\to 0^{+}$, in se dobi formula, veljavna za $\mathrm{\Re }(s)<0$ :

$\eta (s)=-\sin \left(\frac{s\pi }{2}\right)\underset{0}{\overset{\mathrm{\infty }}{\int }}\frac{t^{-s}}{\sinh (\pi t)}\mathrm{d}t.$

Numerični algoritmi

Večina tehnik pospeševanja konvergence vrst razvitih za alternirajoče vrste, se lahko učinkovito uporabi pri računanju Dirichletove funkcije η. Ena še posebej enostavna, vendar smiselna metoda je uporaba Eulerjeve transformcije za alternirajoče vrste, ki da:

$\eta (s)=\sum _{n=0}^{\mathrm{\infty }}\frac{1}{2^{n+1}}\sum _{k=0}^n(-1{)}^k(\genfrac{}{}{0ex}{}{n}{k})\frac{1}{(k+1{)}^s}.$

Druga notranja vsota je vnaprejšnja razlika.

Borweinova metoda

Borwein je uporabil približke s pomočjo polinomov Čebišova in razdelal metodo z učinkovito računanje Dirichletove funkcije η. Če je:

$d_k=n\sum _{i=0}^k\frac{(n+i-1)!4^i}{(n-i)!(2i)!}$

potem je:

$\eta (s)=-\frac{1}{d_n}\sum _{k=0}^{n-1}\frac{(-1{)}^k(d_k-d_n)}{(k+1{)}^s}+{\gamma }_n(s),$

kjer je za $\mathrm{\Re }(s)\ge \frac{1}{2}$ člen napake γ_n omejen z:

$|{\gamma }_n(s)|\le \frac{3}{(3+\sqrt{8}{)}^n}(1+2|\mathrm{\Im }(s)|)\exp (\frac{\pi }{2}|\mathrm{\Im }(s)|).$

Faktor $3+\sqrt{8}\approx 5,8$ v meji napake nakazuje, da Borweinova vrsta konvergira precej hitro, ko se n povečuje.

Značilnosti

Dirichletova funkcija $\eta$ je povezana z Riemannovo funkcijo ζ in Dirichletovo funkcijo λ kot:

$\frac{\eta (s)}{2^s-2}=\frac{\zeta (s)}{2^s}=\frac{\lambda (s)}{2^s-1}$

in:

$\eta (s)=\zeta (s)-2\lambda (s).$

Posebne vrednosti

$\eta (-1)=\frac{1}{4}=0,25,$ Abelova vsota vrste 1 − 2 + 3 − 4 + ···.

$\eta (0)=\frac{1}{2}=0,5,$ Abelova vsota Grandijeve vrste 1 − 1 + 1 − 1 + ···.

za celo število n > 1, če je B_n n-to Bernoullijevo število, potem velja zveza:

$\eta (1-n)=\frac{2^n-1}{n}{B}_n.$

In še nekatere vrednosti:

$\eta (1/2)=-(\sqrt{2}-1)\zeta (1/2)=0,604898643421\dots ,$ Predloga:OEIS.

$\eta (1)=\ln 2=0,693147180559\dots ,$ alternirajoča harmonična vrsta 1 − 1/2 + 1/3 − 1/4 + ··· Predloga:OEIS.

$\eta (3/2)=-\frac{1}{2}(\sqrt{2}-2)\zeta (3/2)=0,765147024625\dots .$

$\eta (2)=\frac{{\pi }^2}{12}=0,822467033424\dots ,$ Predloga:OEIS.

$\eta (5/2)=-\frac{1}{4}(\sqrt{2}-4)\zeta (5/2)=0,867199889012\dots .$

$\eta (3)=\frac{3}{4}\zeta (3)=0,901542677369\dots ,$ Predloga:OEIS.

$\eta (7/2)=-\frac{1}{8}(\sqrt{2}-8)\zeta (7/2)=0,927553577773\dots .$

$\eta (4)=\frac{7{\pi }^4}{720}=0,947032829497\dots .$

$\eta (5)=\frac{15}{16}\zeta (5)=0,972119770446\dots .$

$\eta (6)=\frac{31{\pi }^6}{30240}=0,985551091297\dots .$

$\eta (7)=\frac{63}{64}\zeta (7)=0,992593819922\dots .$

$\eta (8)=\frac{127{\pi }^8}{1209600}=0,996233001852\dots .$

$\eta (9)=\frac{255}{256}\zeta (9)=0,998094297541\dots .$

$\eta (10)=\frac{73{\pi }^{10}}{6842880}=0,999039507598\dots .$

$\eta (11)=\frac{1023}{1024}\zeta (11)=0,999517143498\dots .$

$\eta (12)=\frac{1414477{\pi }^{12}}{1307674368000}=0,999757685143\dots .$

Splošna oblika za soda pozitivna cela števila je:

$\eta (2n)=(-1{)}^{n+1}\frac{B_{2n}{\pi }^{2n}(2^{2n-1}-1)}{(2n)!}.$

Za liha pozitivna cela števila velja zveza :

$\eta (2n+1)=(1-\frac{1}{2^{2n}})\zeta (2n+1),(n\ge 1).$

Odvajanje

Odvod po parametru s je za $s\ne 1$ dan v splošnem:

${\eta }^{\prime }(s)\equiv \frac{\mathrm{d}}{\mathrm{d}s}\eta (s)=\sum _{n=1}^{\mathrm{\infty }}\frac{(-1{)}^n\ln n}{n^s}=2^{1-s}\ln (2)\zeta (s)+(1-2^{1-s})\frac{\mathrm{d}}{\mathrm{d}s}\zeta (s),$

in posebej:

${\eta }^{\prime }(1)\equiv \frac{\mathrm{d}}{\mathrm{d}s}\eta (1)=\sum _{n=1}^{\mathrm{\infty }}\frac{(-1{)}^n\ln n}{n}=\gamma \ln 2-\frac{1}{2}\ln (2{)}^2=0,159868903742\dots ,$ Predloga:OEIS.

Glej tudi

• 1 − 2 + 3 − 4 + ···+

Viri

• Predloga:Navedi arXiv
• Predloga:Citat
• Predloga:Citat
• Predloga:Citat
• Predloga:Citat
• Predloga:Citat
• Predloga:Citat (Druga izdaja Chelsea, New York, 1953, str. 160, 933)
• Predloga:Citat
• Predloga:Citat
• Predloga:Citat
• Predloga:Citat
• Predloga:Citat
• Predloga:Citat
• Predloga:Citat