Harmonična vrsta

Predloga:Infinitezimalni račun Harmónična vŕsta je v matematiki divergentna vrsta:

$\sum _{n=1}^{\mathrm{\infty }}\frac{1}{n}=1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\cdots .$

Tako se imenuje, ker so valovne dolžine delnih tonov nihajoče strune sorazmerne z 1, 1/2, 1/3, 1/4, ··· . Vsak člen vrste za prvim je harmonična sredina sosednjih dveh členov, predhodnega in naslednjega, $H(a_{n-1},a_{n+1})$. Na primer:

$\frac{1}{2}=\frac{2}{1+\frac{1}{\frac{1}{3}}},\frac{1}{3}=\frac{2}{\frac{1}{\frac{1}{2}}+\frac{1}{\frac{1}{4}}},\frac{1}{4}=\frac{2}{\frac{1}{\frac{1}{3}}+\frac{1}{\frac{1}{5}}},\frac{1}{5}=\frac{2}{\frac{1}{\frac{1}{4}}+\frac{1}{\frac{1}{6}}},\cdots ,\frac{1}{a_n}=\frac{2}{\frac{1}{\frac{1}{a_{n-1}}}+\frac{1}{\frac{1}{a_{n+1}}}}.$

Zaporedje členov s takšnimi značilnostmi je harmonično zaporedje, harmonična vrsta pa je vsota harmoničnega zaporedja (vsota členov harmoničnega zaporedja).

Tudi izraz harmonična sredina izvira iz glasbe.

Vrsta divergira, sicer počasi, k neskončnosti (vsota prvih 10⁴³ členov je manj kot 100). To se lahko lepo pokaže z dejstvom, da je harmonična vrsta po členih večja ali enaka z vrsto:

$\begin{array}{cc}\sum _{n=1}^{\mathrm{\infty }}\frac{1}{n}& =1+\left[\frac{1}{2}\right]+[\frac{1}{3}+\frac{1}{4}]+[\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\frac{1}{8}]+[\frac{1}{9}+\cdots ]+\cdots \\ \sum _{n=1}^{\mathrm{\infty }}\frac{1}{2^{\lceil {\log }_{2}n\rceil }}& =1+\left[\frac{1}{2}\right]+[\frac{1}{4}+\frac{1}{4}]+[\frac{1}{8}+\frac{1}{8}+\frac{1}{8}+\frac{1}{8}]+[\frac{1}{16}+\cdots ]+\cdots \\ & =1+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\cdots ,\end{array}$

ki očitno divergira. Ta dokaz je podal Nicole Oresme v 14. stoletju in predstavlja enega od viškov srednjeveške matematike. Kasneje so dokaze podali Pietro Mengoli, Johann in Jakob Bernoulli v 17. stoletju. Celo vsota obratnih vrednosti praštevil divergira k neskončnosti, čeprav je to težje dokazati.

Konvergenca alternirajoče harmonične vrste

Prvih štirinajst delnih vsot alternirajoče harmonične vrste (črni odseki) kaže njeno konvergenco k naravnemu logaritmu od 2 (rdeča premica)

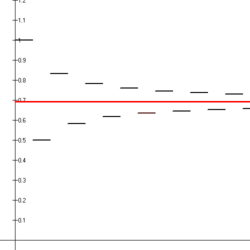
Alternirajoča harmonična vrsta na drugi strani konvergira - je pogojno konvergentna:

$\sum _{n=1}^{\mathrm{\infty }}\frac{(-1{)}^{n+1}}{n}=1-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}+\cdots =\ln 2=0,693147180\dots .$

Konvergenco alternirajoče harmonične vrste je leta 1650 v članku dokazal Mengoli. Ta enakost je posledica Mercatorjeve vrste, Taylorjeve vrste za naravni logaritem. Po obliki Mercatorjevi vrsti sorodna je vrsta:

$\sum _{n=0}^{\mathrm{\infty }}\frac{(-1{)}^n}{2n+1}=1-\frac{1}{3}+\frac{1}{5}-\frac{1}{7}+\cdots =\arctan (1)=\frac{\pi }{4}.$

To je posledica razvoja krožne fukncije arkus tangens v Taylorjevo vrsto, katere konvergenčni polmer je enak 1.

Delne vsote

n-ta delna vsota harmonične vrste:

$H_n=\sum _{k=1}^n\frac{1}{k}$

se imenuje n-to harmonično število.

Razlika med n-tim harmoničnim številom in naravnim logaritmom od n konvergira k Euler-Macheronijevi konstanti:

$\underset{n\to \mathrm{\infty }}{\lim }(H_n-\ln n)=\gamma .$

Razlika med dvema različnima harmoničnima številoma ni nikoli celo število.

Splošna harmonična vrsta

Splošna harmonična vrsta ima obliko:

$\sum _{n=0}^{\mathrm{\infty }}\frac{1}{an+b},$

kjer sta konstanti a in b končni realni števili.

Vse splošne harmonične vrste divergirajo.

Glej tudi

• alikvotni toni