Loksodroma

Slika loksodrome. Spiralno se približuje Severnemu polu.

Slika:LoxodromeConstAngle sl.svg

Loksodroma od A do B seka vse poldnevnike pod istim kotom.

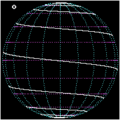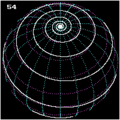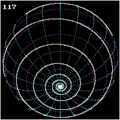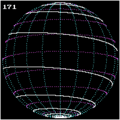
Loksodroma (izraz izvira iz grške besede loxos, kar pomeni nagib in besede drome, kar pomeni smer) je krivulja (pot), ki seka vse poldnevnike pod istim kotom (vendar ne pod pravim kotom). Torej je to krivulja na površini krogle.V splošnem lahko določimo loksodromo na površini vsakega rotacijskega telesa.

Matematična izpeljava enačbe

Naj bo $\beta$ konstantna smer (kurs) od pravega severnega pola loksodrome in naj bo ${\beta }_0$ zemljepisna dolžina kjer loksodroma prečka ekvator. Naj bo tudi $\lambda$ zemljepisna dolžina točke na loksodromi. V Mercatorjevi projekciji je loksodroma ravna črta

$x=\lambda$

$y=m(\lambda -{\lambda }_0)$

z nagibom $m=\cot (\beta )$

Za točko z zemljepisno širino $\varphi$ in zemljepisno dolžino $\lambda$ lahko lego v Mercatorjevi projekciji izrazimo kot

$x=\lambda$
$y={\tanh }^{-1}(\sin \varphi )$.

Potem je zemljepisna širina točke

$\varphi ={\sin }^{-1}(\tanh (m(\lambda -{\lambda }_0))),$

oziroma z uporabo Gudermannove funkcije (oznaka gd) $\varphi =\mathrm{g}\mathrm{d}\mathrm{(}\mathrm{m}\mathrm{(}\mathrm{\lambda }\mathrm{-}{\mathrm{\lambda }}_{\mathrm{0}}\mathrm{)}\mathrm{)}$.

V kartezičnem koordinatnem sistemu se to lahko poenostavljeno piše kot

$x=r\cos (\lambda )/\cosh (m(\lambda -{\lambda }_0)),$

$y=r\sin (\lambda )/\cosh (m(\lambda -{\lambda }_0)),$

$z=r\tanh (m(\lambda -{\lambda }_0)).$

• 
  Animacija s prikazom loksodrome
• 
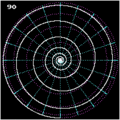
  Potek loksodrome na polu
• 
  Potek loksodrome na ekvatorju

Slika:LoxodromeOrthodrome sl.svg

Primerjava loksodrome in ortodrome.

Zgodovina

Prvi se je z loksodromo ukvarjal portugalski matematik, izumitelj, zdravnik, astronom, pedagog in geograf Pedro Nunes (1502 – 1578). Njegovo delo je nadaljeval angleški matematik in astronom Thomas Harriot (1560 – 1621).

Značilnosti

• loksodroma je na zemljevidih, ki so izdelani v Mercatorjevi projekciji ravna črta.
• loksodroma ni najkrajša razdalja med dvema točkama na sferi, najkrajša razdalja je del velikega kroga
• loksodroma je neskončno dolga krivulja
• loksodroma je določena z zemljepisno širino in dolžino točke na krivulji in s kotom, ki ga tvori s poldnevniki.
• kadar je kot pod katerim seka krivulja poldnevnike enak 0º ali 90º loksodroma nima zaključka

Glej tudi

• veliki krog
• mali krog
• ortodroma

Zunanje povezave

• Loksodroma na MathWorld Predloga:Ikona en
• Loksodroma na MathPages Predloga:Ikona en
• Mercatorjeva projekcija Predloga:Ikona en
• Nekaj problemov iz navigacije Predloga:Ikona fr
• Loksodroma Predloga:Webarchive na PlanetMath Predloga:Ikona en