Pravokotnost

Konstrukcija pravokotnice na premico AB iz dane točke C

Predloga:Splošna geometrija Pravokótnost (tudi ortogonálnost) je ena od osnovnih relacij med različnimi geometrijskimi objekti: premicami, daljicami, vektorji, krivuljami, ravninami ipd. Pravokotnost označimo s simbolom $\mathrm{\perp }$.

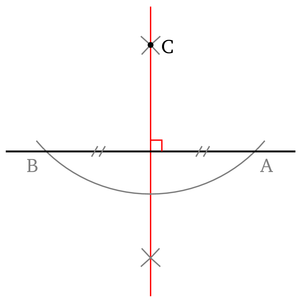
Premici sta pravokotni, če se sekata tako, da oklepata pravi kot - to je kot, ki je skladen s svojim sokotom (v stopinjah meri 90°). Pravokotni premici torej delita ravnino, v kateri ležita, na štiri med seboj skladne dele.

Premica je pravokotna na ravnino, če je pravokotna na katerokoli premico, ki leži v tej ravnini in poteka skozi prebodišče. Premico, ki je pravokotna na ravnino (ali tudi na krivuljo ali ploskev), imenujemo pravokótnica ali normála.

Ugotavljanje pravokotnosti

Če pravokotni premici v kartezični ravnini zapišemo z enačbama $p:y=k_{1}x+n_1$ in $q:y=k_{2}x+n_2$, potem za smerna koeficienta premic velja: $k_1=-\frac{1}{k_2}$.

Krivulji sta pravokotni, če sta pravokotni njuni tangenti v presečišču. Če sta krivulji podani kot grafa funkcij, lahko preverimo pravokotnost tako, da z odvodom izračunamo smerna koeficienta obeh tangent in ugotovimo, če velja zveza $k_1=-\frac{1}{k_2}$.

Vektorja sta pravokotna, samo če je njun skalarni produkt enak 0. (Pri tem privzamemo, da je ničelni vektor $\overrightarrow{\mathrm{𝟎}}$ pravokoten na vse vektorje in je hkrati edini vektor, ki je pravokoten sam nase.)

$\overrightarrow{𝐚}\mathrm{\perp }\overrightarrow{𝐛}⟺\overrightarrow{𝐚}\cdot \overrightarrow{𝐛}=0.$

Glej tudi

• vzporednost
• ortogonalnost