Sokrožne točke

Sòkróžne tóčke (tudi koncíklične tóčke) so v geometriji točke, ki ležijo na isti krožnici.

Sokrožne točke kažejo, da se simetrali parov točk sekata v isti točki, oziroma da tvorita šop

Štiri sokrožne točke, kjer sta kota $\alpha$ enaka. Točke tvorijo oglišča tetivnega štirikotnika

Trikotniku lahko očrtamo krog. Štirikotnik, ki mu lahko očrtamo krog, je tetivni štirikotnik.

V splošnem mora biti središče kroga S, na katerem ležita točki A in B, takšno, da sta dolžini SA in SB enaki. Zaradi tega mora S ležati na simetrali daljice AB. Za n različnih točk je n(n− 1)/2 takšnih premic, in vse se morajo sekati v isti točki.

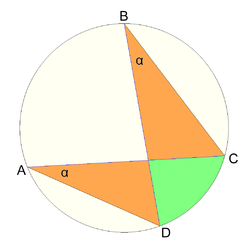
V tetivnem štirikotniku so vsa njegova oglišča sokrožna. V splošnem so mnogokotniki, ki imajo vsa oglišča sokrožna, tetivni mnogokotniki. Poljubne tri nekolinearne točke A, B in C so sokrožne eni sami krožnici. Štiri različne točke A, B, C in D so sokrožne, če velja:

$\alpha \equiv \mathrm{\angle }CAD=\mathrm{\angle }CBD.$

Glej tudi

• kolinearne točke
• Lesterjev izrek