Petriejev mnogokotnik: Razlika med redakcijama
imported>InternetArchiveBot Rescuing 1 sources and tagging 0 as dead.) #IABot (v2.0.9.4 |
(ni razlike)
|
Trenutna redakcija s časom 22:23, 25. maj 2023
Petriejev mnogokotnik za pravilne politope z razsežnostjo je nagnjeni mnogokotnik v katerih vsaka zaporedna stranica (n - 1) pripada eni od facet. Petriejev mnogokotnik pravilnega mnogokotnika je sam po sebi pravilen mnogokotnik. Tako je za pravilni polieder nagnjeni mnogokotnik tisti, ki mu za vsaki dve zaporedni stranici (ne pa tri) pripada ena od stranskih ploskev.[1]
Za vsak pravilni politop obstaja pravokotna projekcija na ravnino tako, da Petriejev mnogokotnik postane pravilni mnogokotnik.
Petriejevi mnogokotniki so neravninski mnogokotniki, katerih robovi so podmnožica robov poliedrov.[2]
Ravnina, ki se jo obravnava, je Coxeterjeva ravnina s simetrijsko grupo mnogokotnika in s številom stranic , ki so Coxeterjeva števila Coxeterjeve grupe. Ti mnogokotniki in projicirani grafi so zelo uporabni za predstavo o strukturi simetrije za politope v višjih razsežnostih.
Zgodovina
John Flinders Petrie (1907–1972) je bil prvi, ki je spoznal pomembnost poševnih mnogokotnikov. Po njem se tudi imenujejo mnogokotniki. Bil je edini sin egiptologa Flindersa Petrieja (1853–1942).
Petriejevi mnogokotniki pravilnih poliedrov
Petriejev mnogokotnik pravilnega poliedra {p, q} s h stranicami je:
- cos2(π/h) = cos2(π/p) + cos2(π/q).
Pravilna duala {p, q} in {q, p} sta v istem projiciranem Petriejevem mnogokotniku.

| ||||
| tetraeder | kocka | oktaeder | dodekaeder | ikozaeder |
| Predloga:CDD | Predloga:CDD | Predloga:CDD | Predloga:CDD | Predloga:CDD |
| centrirano na stranico | centrirano na oglišče | centrirano na stransko ploskev | centrirano na stransko ploskev | centrirano na oglišče |
| 4 stranice | 6 stranic | 6 stranic | 10 stranic | 10 stranic |
| V:(4,0) | V:(6,2) | V:(6,0) | V:(10,10,0) | V:(10,2) |
| Petriejevi mnogokotniki so zunanjost teh ortogonalnih projekcij. Modro kaže "sprednje" robove, črne črte kažejo zadnje robove. Koncentrični obroč oglišč se šteje od zunanje strani navznoter z oznako: V:(a, b, ...) in se konča z nič, če ni središčnega oglišča. | ||||
Petriejevi mnogokotniki pravilnih polihoronov (4-politopov)
 {3,3,3} Predloga:CDD 5-celica 5 stranskih ploskev V:(5,0) |
 {3,3,4} Predloga:CDD 16-celica 8 stranskih ploskev V:(8,0) |
 {4,3,3} Predloga:CDD teserakt 8 stranskih ploskev V:(8,8,0) |
 {3,4,3} Predloga:CDD 24-celica 12 stranskih ploskev V:(12,6,6,0) |
 {5,3,3} 120-celica 30 stranskih ploskev V:((30,60)3,603,30,60,0) |
 {3,3,5} 600-celica 30 stranskih ploskev V:(30,30,30,30,0) |
Projekcije Petriejevih mnogokotnikov pravilnih in uniformnih politopov
Projekcije Petriejevih mnogokotnikov so ena izmed najbolj uporabnih načinov za prikaz politopov, ki imajo razsežnost štiri in več. V spodnji preglednici so prikazane projekcije Petriejevih mnogokotnikov treh družin simpleksov, hiperkock in ortopleksov ter posebnih Liejevih grup En, ki generirajo polpravilne in uniformne politope za razsežnosti od 4 do 8.
| Coxeterjeva grupa | An | BCn | Dn |
|
Hn | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 |  trikotnik |
 kvadrat |
 šestkotnik |
 petkotnik | ||||||||||
| 3 |  tetraeder |
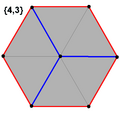 kocka |
 oktaeder |
 tetraeder |
 dodekaeder |
 ikozaeder | ||||||||
| 4 |  5-celica |
 teserakt |
 16-celica |
 polteserakt |
 24-celica |
 120-celica |
 600-celica | |||||||
| 5 |  5-simpleks |
 5-kocka |
 5-ortopleks |
 5-polkocka |
||||||||||
| 6 |  6-simpleks |
 6-kocka |
 6-ortopleks |
 6-polkocka |
 122 |
 221 |
||||||||
| 7 |  7-simpleks |
 7-kocka |
 7-ortopleks |
 7-polkocka |
 132 |
 231 |
 321 |
|||||||
| 8 |  8-simpleks |
 8-kocka |
 8-ortopleks |
 8-polkocka |
 142 |
 241 |
 421 |
|||||||
| 9 |  9-simpleks |
 9-kocka |
 9-ortopleks |
 9-polkocka | ||||||||||
| 10 |  10-simpleksPredloga:CDD 10-simpleksPredloga:CDD
|
 10-kocka 10-kocka
|
 10-ortopleks 10-ortopleks
|
 10-polkocka 10-polkocka
| ||||||||||
| družina n |
n-simpleks | n-hiperkocka | n-ortopleks | n-polkocka | 1k2 | 2k1 | k21 | |||||||
Sklici
Zunanje povezave
- Predloga:MathWorld
- Predloga:MathWorld
- Petriejev mnogokotnik na WolframAlpha Predloga:Ikona en
- ↑ Kaleidoscopes: Selected Writings of H. S. M. Coxeter, editied by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1] (Definicija: listina 13, Diskretne grupe generirane z zrcaljenjem, 1933, s. 161)
- ↑ Predloga:Navedi splet