Absolutni izsev

Absolútni izsèv, oziroma absolútna magnitúda je v astronomiji sij zvezde, kakršen je v resnici in ne kot ga vidimo z Zemlje.

Gre za standard, ki nam pove, kako svetla bi bila posamezna zvezda, če bi jo postavili na oddaljenost 10 parsekov (10 · 3,26 svetlobnih let), oziroma kakšen bi bil njen navidezni sij. Absolutni izsev je lahko dobro izhodišče za izračun mase zvezde. Razmerje med količnikom izseva zvezde in izseva Sonca je enako razmerju med maso zvezde in Sončevo maso, pri čemer sta slednja podana s koeficientom a. Za zvezde iz glavnega niza ta znaša 3 (to je bilo potrjeno za vse zvezde svetlostnega razreda V). Če torej poznamo izsev zvezde, lahko izračunamo njeno maso. Ta znaša vrednost izseva zvezde na potenco 1/3, kar je 0,33. Pri drugih zvezdah, orjakinjah vseh vrst (I, I-0, II-a, II-b, III) in zvezdah drugih spektralnih razredov kot V (IV, VI, VII) je koeficient 2/7.

Zvezde imajo absolutni izsev od skoraj -90,00 pa vse do 17,00.

Za absolutni izsev velja enak dogovor kot za navidezni sij, razlika med stopnjami svetlosti je ~2,51 (saj je 2,51⁵ ≈ 100). Absolutni izsev naše Galaksije je na primer približno -20,5. Kvazar z absolutnim izsevom -25,5 je stokrat svetlejši kot naša galaksija. Če bi lahko hkrati na isti razdalji videli kvazar in našo Galaksijo, bi bil kvazar za 5 velikostnih razredov (magnitud) (oziroma 100-krat) svetlejši od naše Galaksije.

Umovanje o koeficientu a

Gre za dve možnosti. Koeficient a je lahko stalen in nespremenljiv, ali pa se spreminja. V veljavi je dejstvo, da znaša a pri običajnih zvezdah, ki so pritlikave in bolj ali manj podobne Soncu (so spektralnega razreda V), 3, kar pomeni, da njegova masa raste s tretjo potenco. Tako se da na hitro ugotoviti, da znaša vrednost mase zvezde med 0,08 in približno 63,00 mas Sonca. Čeprav naj bi bil prag zvezd po nekaterih merilih znašal celo 155,00 mas Sonca.

Zvezda z desetimi sončevimi masami bi torej imela izsev približno 1000. Zvezda s 63 Sončevimi masami pa 265.000 izsevov Sonca. Vsemu navkljub pa ta odnos ne velja za druge zvezde, kot so to npr. orjakinje vseh vrst. Pri teh se dejanski masi bolj prilega vrednost 3,5, kar pomeni, da njihova masa narašča s potenco sedmih polovic.

Če se vrednost a spreminja za najmanj masivne in najbolj masivne zvezde, pa veljajo vrednosti: da pri orjakinjah a znaša 1,6; kar pomeni, da njihova masa narašča. Pri pritlikavih zvezdah pa znaša vrednost a 4,8.

Telesa Osončja (H)

Predloga:Anchor Predloga:For

Abs. mag (H)
in premer
za asteroide
(albedo=0,15)^[1]
H	Premer
10	34 km
12,6	10 km
15	3,4 km
17,6	1 km
19,2	500 metrov
20	340 metrov
22,6	100 metrov
24,2	50 metrov
25	34 metrov
27,6	10 metrov
30	3,4 metrov

Za planete in asteroide je definicija absolutne magnitude še drugačna (prav tako za vse ostale objekte razen Sonca in Zemlje v Osončju). Ta absolutna magnituda, imenovana tudi $H$ , je definirana kot navidezna magnituda, ki bi jo imelo telo v idealni sončevi opoziciji (postavitev, ki je v praksi nemogoča), če bi bilo od Sonca in od opazovalca naenkrat oddaljeno natanko 1 astronomsko enoto (AU).^[2] Telesa Osončja so osvetljena s Soncem, in se torej magnituda spreminja kot funkcija v pogojih osvetljevanja, opisana kot fazni kot. To razmerje se pogosto imenuje fazna krivulja. Absolutna magnituda je svetlost v faznem kotu nič, v položaju imenovanem tudi opozicija.

Navidezna magnituda

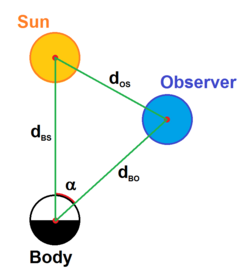
Absolutna magnituda $H$ se lahko uporabi za izračun navidezne magnitude telesa $m$ . Za telo, ki odbija sončevo svetlobo, sta $H$ in $m$ povezana z naslednjo relacijo

m = H + 5 \log_{10} (\frac{d_{B S} d_{B O}}{d_{0}^{2}}) - 2, 5 \log_{10} q (α),

kjer je $α$ fazni kot, ki je kot med telesom, Soncem in opazovalcem. $q (α)$ je fazni integral (integriranje odbite svetlobe; število na intervalu 0 do 1).^[3]

Po kosinusnem izreku dobimo:

\cos α = \frac{d_{B O}^{2} + d_{B S}^{2} - d_{O S}^{2}}{2 d_{B O} d_{B S}} .

Razdalje:

Predloga:Math je razdalja med telesom in opazovalcem
Predloga:Math je razdalja med telesom in Soncem
Predloga:Math je razdalja med opazovalcem in Soncem
Predloga:Math je 1 AU, povprečna razdalja med Zemljo in Soncem

Približki faznega integrala $q (α)$

Vrednost $q (α)$ je odvisna od lastnosti površine, ki odbija svetlobo, v posebnem od odbojnosti površine. V praksi, se uporabljajo različni približki, ki temeljijo na znanih ali pričakovanih lastnostih površine.^[3]

Planeti

Planetarna telesa se lahko približajo z idealno difuzno odbijajočimi kroglami. Naj bo $α$ fazni kot v stopinjah, potem^[4]

q (α) = \frac{2}{3} ((1 - \frac{α}{18 0^{\circ}}) \cos α + \frac{1}{π} \sin α) .

Difuzna krogla v polni fazi odbije dve tretjini svetlobe ploščatega diska enakega premera. Četrt faze ( $α = 9 0^{\circ}$ ) ima $\frac{1}{π}$ toliko svetlobe, kot pri polni fazi ( $α = 0^{\circ}$ ).

Za razliko od tega je difuzni ploščati odbojni model preprosto $q (α) = \cos α$ , kar ni realistično, a upošteva opozicijski pojav za grobe površine, ki odbijajo več uniformne svetlobe nazaj na majhnih faznih kotih.

Definicija za geometrični albedo $p$ , merilo za odbojnost planetarnih površin, temelji na difuznem ploščatem odbojnem modelu. Absolutna magnituda $H$ , premer $D$ (v kilometrih)in geometrični albedo $p$ telesa so podani z^[5]^[6]

D = \frac{1329}{\sqrt{p}} \times 1 0^{- 0, 2 H}

km.

primer: Lunina absolutna magnituda $H$ se lahko izračuna iz njenega premera $D = 3474 km$ in geometričnega albeda $p = 0, 113$ :^[7]

H = 5 \log_{10} \frac{1329}{3474 \sqrt{0.113}} = + 0, 28 .

Dobimo $d_{B S} = 1 AU$ , $d_{B O} = 384400 km = 0, 00257 AU .$ Na prvem/zadnjem krajcu, je $q (α) \approx \frac{2}{3 π}$ (sodeč po difuznem odbojnem modelu), ki poda navidezno magnitudo $m = + 0, 28 + 5 \log_{10} (1 \cdot 0, 00257) - 2, 5 \log_{10} (\frac{2}{3 π}) = - 10, 99 .$ . Resnična magnituda je nekoliko nižja, $m = - 10, 0$ . Fazna krivulja Lune je preveč zapletena za difuzni odbojni model.^[8]

Bolj napredni modeli

Ker telesa Osončja niso nikoli popolni difuzni odbojniki, uporabljajo astronomi različne modele za napovedovanje navideznih magnitud na osnovi znanih ali predpostavljenih lastnosti telesa.^[3] Za planete je bil približek za popravljalni del $- 2, 5 \log_{10} q (α)$ v formuli za Predloga:Mvar izpeljan empirično, da bi ustrezal opazovanjih na različnih faznih kotih. Približki, ki jih priporoča Astronomski almanah^[9] so (z $α$ v stopinjah):

Planet	$H$	Približek za $- 2.5 \log_{10} q (α)$
Merkur	−0,613	$+ 6, 328 \times 1 0^{- 2} α - 1, 6336 \times 1 0^{- 3} α^{2} + 3, 3644 \times 1 0^{- 5} α^{3} - 3, 4265 \times 1 0^{- 7} α^{4} + 1, 6893 \times 1 0^{- 9} α^{5} - 3, 0334 \times 1 0^{- 12} α^{6}$
Venera	−4,384	$- 1, 044 \times 1 0^{- 3} α + 3, 687 \times 1 0^{- 4} α^{2} - 2, 814 \times 1 0^{- 6} α^{3} + 8, 938 \times 1 0^{- 9} α^{4}$ (za $0^{\circ} < α \leq 163, 7^{\circ}$ ) $+ 240, 44228 - 2, 81914 α + 8, 39034 \times 1 0^{- 3} α^{2}$ (za $163, 7^{\circ} < α < 17 9^{\circ}$ )
Zemlja	−3,99	$- 1, 060 \times 1 0^{- 3} α + 2, 054 \times 1 0^{- 4} α^{2}$
Mars	−1,601	$+ 2, 267 \times 1 0^{- 2} α - 1, 302 \times 1 0^{- 4} α^{2}$ (za $0^{\circ} < α \leq 5 0^{\circ}$ ) $+ 1, 234 - 2, 573 \times 1 0^{- 2} α + 3, 445 \times 1 0^{- 4} α^{2}$ (za $5 0^{\circ} < α \leq 12 0^{\circ}$ )
Jupiter	−9,395	$- 3, 7 \times 1 0^{- 4} α + 6, 16 \times 1 0^{- 4} α^{2}$ (za $α \leq 1 2^{\circ}$ ) $- 0, 033 - 2, 5 \log_{10} (1 - 1, 507 (\frac{α}{18 0^{\circ}}) - 0, 363 {(\frac{α}{18 0^{\circ}})}^{2} - 0, 062 {(\frac{α}{18 0^{\circ}})}^{3} + 2, 809 {(\frac{α}{18 0^{\circ}})}^{4} - 1, 876 {(\frac{α}{18 0^{\circ}})}^{5})$ (za $α > 1 2^{\circ}$ )
Saturn	−8,914	$1, 825 \sin (β) + 2, 6 \times 1 0^{- 2} α - 0, 378 \sin (β) e^{- 2, 25 α}$ (za planet in prstane, $α < 6, 5^{\circ}$ in $β < 2 7^{\circ}$ ) $- 0, 036 - 3, 7 \times 1 0^{- 4} α + 6, 16 \times 1 0^{- 4} α^{2}$ (za samo kroglo, $α \leq 6^{\circ}$ ) $+ 0, 026 + 2, 446 \times 1 0^{- 4} α + 2, 672 \times 1 0^{- 4} α^{2} - 1, 505 \times 1 0^{- 6} α^{3} + 4, 767 \times 1 0^{- 9} α^{4}$ (za samo kroglo, $6^{\circ} < α < 15 0^{\circ}$ )
Uran	−7,110	$- 8, 4 \times 1 0^{- 4} ϕ^{'} + 6, 587 \times 1 0^{- 3} α + 1, 045 \times 1 0^{- 4} α^{2}$ (za $α < 3, 1^{\circ}$ )
Neptun	−7,00	$+ 7, 944 \times 1 0^{- 3} α + 9, 617 \times 1 0^{- 5} α^{2}$ (za $α < 13 3^{\circ}$ in $t > 2000, 0$ )

Tukaj je $β$ površinska inklinacija Saturnovih prstanov (njihov naklon glede na opazovalca), ki se, videna z Zemlje, spreminja med 0° and 27° skozi eno Saturnovo orbito. $ϕ^{'}$ je majhen popravek, ki je odvisen od Uranovih pod-Zemeljiskih in pod-Solarnih širin. $t$ je leto našega štetja. Neptunova absolutna magnituda se rahlo spreminja zaradi sezonskih pojavov, ko se planet pomika po svoji 165-letni tirnici okoli Sonca, približek pa je veljaven le po letu 2000. Za nekaj pogojev, recimo $α \geq 17 9^{\circ}$ za Venero, je nedostopnih, zato je fazna krivulja v teh primerih neznana.

Primer: Na 1 januar 2019 je bila Venera od Sonca oddaljena $d_{B S} = 0, 719 AU$ , od Zemlje pa $d_{B O} = 0, 645 AU$ . Takrat je bila v faznem kotu $α = 93, 0^{\circ}$ (blizu faze krajca (četrtina)). Pod pogoji polne faze bi imela Venera magnitudo $m = - 4, 384 + 5 \log_{10} (0, 719 \cdot 0, 645) = - 6, 09 .$ Če upoštevamo kot veliko faze, nam izraz za popravek poda resnično navidezno magnitudo $m = - 6, 09 + (- 1, 044 \times 1 0^{- 3} \cdot 93, 0 + 3, 687 \times 1 0^{- 4} \cdot 93, 0^{2} - 2, 814 \times 1 0^{- 6} \cdot 93, 0^{3} + 8, 938 \times 1 0^{- 9} \cdot 93, 0^{4}) = - 4, 59 .$ To je blizu vrednosti $m = - 4, 62$ ki jo je napovedal Jet Propulsion Laboratory.^[10]

Zemljin albedo se spreminja s faktorjem 6, od 0,12 v brez-oblačnem primeru, do 0,76 v primeru altostratusi. Absolutna magnituda tukaj predstavlja albedo 0,434. Zemljina navidezna magnituda se ne more predvideti tako natančno, kot za ostale planete.^[9]

Asteroidi

Če ima telo atmosfero, odseva svetlobo manj ali več izotropno v vse smeri, njegova svetlost pa se lahko izračuna kot difuzni odbojnik. Telesa brez atmosfere, kot asteroidi in lune, odsevajo svetlobo močneje v eno smer, njihova svetlost pa se zelo spreminja, ko se fazni kot približuje $0^{\circ}$ . To hitro svetlenje se imenuje opozicijski pojav. Njegova svetlost je odvisna od fizikalnih lastnosti površine telesa, in se torej razlikuje od asteroida do asteroida.^[3]

Leta 1985 je IAU sprejela pol-empirični sistem $H G$ , ki temelji na dveh parametrih $H$ in $G$ , ki se imenujeta absolutna magnituda in naklon, da ustvari model za opozicijski pojav za efemeride, ki jih je objavil Center malih planetov.^[11]

m = H + 5 \log_{10} (\frac{d_{B S} d_{B O}}{d_{0}^{2}}) - 2, 5 \log_{10} q (α),

kjer

fazni integral je

q (α) = (1 - G) ϕ_{1} (α) + G ϕ_{2} (α)

in

ϕ_{i} (α) = \exp (- A_{i} {(\tan \frac{α}{2})}^{B_{i}})

za

i = 1

ali

2

,

A_{1} = 3, 332

,

A_{2} = 1, 862

,

B_{1} = 0, 631

in

B_{2} = 1, 218

.^[12]

Ta povezava velja za fazne kote $α < 12 0^{\circ}$ , najbolje pa drži, ko je $α < 2 0^{\circ}$ .^[13]

Naklonski parameter $G$ pove velikost opozicije, največkrat Predloga:Val, ko je telo blizu opozicije. Natančno je poznan le za majhno število asteroidov, torej je predpostavljen za večino asteroidov z $G = 0, 15$ .^[13] V redkih primerih je lahko $G$ tudi negativen.^[12]^[14] Primer je 101955 Bennu, z $G = - 0, 08$ .^[15]

Leta 2012 je bil sistem $H G$ uradno zamenjan z izboljšanim sistemom s tremi parametri $H$ , $G_{1}$ in $G_{2}$ , ki ustvari še bolj natančne rezultate, če je opozicijski pojav zelo majhen ali omejen na majhne fazne kote. A leta 2019 sistema $H G_{1} G_{2}$ ni odobril niti Center za male planete, niti Jet Propulsion Laboratory.^[3]^[16]

Navidezna magnituda asteroidov se spreminja med vrtenjem na časovnih intervalih nekaj sekund do nekaj tednov, odvisno od njihove rotacijske periode, tudi do $2 mag$ ali več.^[17] Njihova magnituda se lahko spreminja tudi z opazovalne smeri, odvisno od njihovega osnega naklona. V veliko primerih ni znana niti rotacijska perioda, niti osni naklon, kar omejuje napovedi. Predstavljeni modeli tukaj ne zajemajo takšnih pojavov.^[3]^[13]

Magnitude kometov

Svetlost kometa se podaja ločeno kot celotna magnituda ( $m_{1}$ , svetlost, integrirana skozi celotni vidni podaljšek kome) in magnituda jedra ( $m_{2}$ , samo svetlost središčnega območja).^[18] Obe sta drugačni lestvici kot magnitude za planete in asteroide in ne se morejo primerjati z absolutno magnitudo asteorida Predloga:Mvar.

Aktivnost kometov se spreminja z njihovo oddaljenostjo od Sonca. Njihova svetlost se lahko približa z

m_{1} = M_{1} + 2, 5 \cdot K_{1} \log_{10} (\frac{d_{B S}}{d_{0}}) + 5 \log_{10} (\frac{d_{B O}}{d_{0}})

m_{2} = M_{2} + 2, 5 \cdot K_{2} \log_{10} (\frac{d_{B S}}{d_{0}}) + 5 \log_{10} (\frac{d_{B O}}{d_{0}}),

kjer sta $m_{1, 2}$ zaporedoma navidezna celotna magnituda in magnituda jedra, $M_{1, 2}$ sta "absolutna" celotna magnituda in magnituda jedra, $d_{B S}$ in $d_{B O}$ sta razdalji telo-Sonce in telo-opazovalec, $d_{0}$ je astronomska enota in $K_{1, 2}$ sta naklonska parametra, ki ponazarjata kometovo aktivnost. Za $K = 2$ se to posploši na popolnoma odsevno telo.^[19]

Na primer svetlobna krivulja kometa C/2011 L4 (PANSTARRS) se lahko približa z $M_{1} = 5, 41, K_{1} = 3, 69 .$ ^[20] Na dan prehoda perihelija, 10. marca 2013, je bil komet PANSTARRS od Sonca oddaljen $0, 302 AU$ in $1, 109 AU$ od Zemlje. Celotno navidezna magnituda $m_{1}$ se je takrat napovedala $m_{1} = 5, 41 + 2, 5 \cdot 3, 69 \cdot \log_{10} (0, 302) + 5 \log_{10} (1, 109) = + 0, 8$ . The Minor Planet Center poda podobno vrednost, $m_{1} = + 0, 5$ .^[21]

Absolutne magnitude in velikosti jeder kometov
Komet	Absolutna magnituda $M_{1}$ ^[22]	Premer jedra
Komet Sarabat	−3,0	≈100 km?
Komet Hale-Bopp	−1,3	60 ± 20 km
Halleyjev komet	4,0	14,9 x 8,2 km
povprečni novi komet	6,5	≈2 km^[23]
289P/Blanpain (med izbruhom 1819)	8,5^[24]	320 m^[25]
289P/Blanpain (normalna aktivnost)	22,9^[26]	320 m

Absolutna magnituda kateregakoli kometa se lahko dramatično spreminja. Lahko se spremeni skupaj s spremembo njegove aktivnost, ali če je komet v fazi izbruha. To naredi absolutno magnitudo težko za ocenjevanje velikosti. Ko je bil leta 1819 odkrit komet 289P/Blanpain, je bila njegova absolutna magnituda ocenjena na $M_{1} = 8, 5$ .^[24] Kasneje so komet izgubili, odkrili so ga šele leta 2003. Takrat je njegova absolutna magnituda padla na $M_{1} = 22, 9$ ,^[26] leta 1819 pa je bil komet v fazi izbruha. Leta 1819 je 289P/Blanpain dosegel svetlost za opazovanje s prostim očesom (5–8 mag), četudi je to eden izmed kometov z najmanjšimi jedri, ki so se kadarkoli fizično zaznali. Takšni kometi po navadi niso nikoli svetlejši od 18 mag.^[24]^[25]

Za nekatere komete, ki so jih opazovali na dovolj velikih heliocentričnih razdaljah, da se loči svetlobo, ki je odbita od kome in samega jedra, so izračunali velikost, ki je analogna tisti za asteroide.^[27]

Glej tudi

navidezni sij

Predloga:Portal

Sklici

Predloga:Reflist

Predloga:Normativna kontrola

↑ CNEOS približek velikosti asteroidov
↑ Napaka pri navajanju: Neveljavna značka <ref>; sklici, imenovani Luciuk, ne vsebujejo nobenega besedila
↑ ^3,0 ^3,1 ^3,2 ^3,3 ^3,4 ^3,5 Napaka pri navajanju: Neveljavna značka <ref>; sklici, imenovani Karttunen2016, ne vsebujejo nobenega besedila
↑ Napaka pri navajanju: Neveljavna značka <ref>; sklici, imenovani Whitmell1907, ne vsebujejo nobenega besedila
↑ Napaka pri navajanju: Neveljavna značka <ref>; sklici, imenovani sizemagnitude, ne vsebujejo nobenega besedila
↑ Napaka pri navajanju: Neveljavna značka <ref>; sklici, imenovani Mag_formula, ne vsebujejo nobenega besedila
↑ Napaka pri navajanju: Neveljavna značka <ref>; sklici, imenovani Albedo, ne vsebujejo nobenega besedila
↑ Napaka pri navajanju: Neveljavna značka <ref>; sklici, imenovani Luciuk2, ne vsebujejo nobenega besedila
↑ ^9,0 ^9,1 Napaka pri navajanju: Neveljavna značka <ref>; sklici, imenovani Mallama_and_Hilton, ne vsebujejo nobenega besedila
↑ Napaka pri navajanju: Neveljavna značka <ref>; sklici, imenovani JPLHorizonsVenus, ne vsebujejo nobenega besedila
↑ Napaka pri navajanju: Neveljavna značka <ref>; sklici, imenovani MPC1985, ne vsebujejo nobenega besedila
↑ ^12,0 ^12,1 Napaka pri navajanju: Neveljavna značka <ref>; sklici, imenovani Lagerkvist, ne vsebujejo nobenega besedila
↑ ^13,0 ^13,1 ^13,2 Napaka pri navajanju: Neveljavna značka <ref>; sklici, imenovani dymock, ne vsebujejo nobenega besedila
↑ Napaka pri navajanju: Neveljavna značka <ref>; sklici, imenovani JPLdoc, ne vsebujejo nobenega besedila
↑ Napaka pri navajanju: Neveljavna značka <ref>; sklici, imenovani Bennu, ne vsebujejo nobenega besedila
↑ Napaka pri navajanju: Neveljavna značka <ref>; sklici, imenovani Shevchenko2016, ne vsebujejo nobenega besedila
↑ Napaka pri navajanju: Neveljavna značka <ref>; sklici, imenovani lc, ne vsebujejo nobenega besedila
↑ Napaka pri navajanju: Neveljavna značka <ref>; sklici, imenovani MPES, ne vsebujejo nobenega besedila
↑ Napaka pri navajanju: Neveljavna značka <ref>; sklici, imenovani Meisel1976, ne vsebujejo nobenega besedila
↑ Napaka pri navajanju: Neveljavna značka <ref>; sklici, imenovani COBS 2011L4, ne vsebujejo nobenega besedila
↑ Napaka pri navajanju: Neveljavna značka <ref>; sklici, imenovani MPC2011L4, ne vsebujejo nobenega besedila
↑ Napaka pri navajanju: Neveljavna značka <ref>; sklici, imenovani kidger, ne vsebujejo nobenega besedila
↑ Napaka pri navajanju: Neveljavna značka <ref>; sklici, imenovani Hughes, ne vsebujejo nobenega besedila
↑ ^24,0 ^24,1 ^24,2 Napaka pri navajanju: Neveljavna značka <ref>; sklici, imenovani Yoshida, ne vsebujejo nobenega besedila
↑ ^25,0 ^25,1 Napaka pri navajanju: Neveljavna značka <ref>; sklici, imenovani Jewitt, ne vsebujejo nobenega besedila
↑ ^26,0 ^26,1 Napaka pri navajanju: Neveljavna značka <ref>; sklici, imenovani JPL_289, ne vsebujejo nobenega besedila
↑ Napaka pri navajanju: Neveljavna značka <ref>; sklici, imenovani Lamy2004, ne vsebujejo nobenega besedila

[1] CNEOS približek velikosti asteroidov

[Luciuk-2] Napaka pri navajanju: Neveljavna značka <ref>; sklici, imenovani Luciuk, ne vsebujejo nobenega besedila

[Karttunen2016-3] 3,0 ^3,1 ^3,2 ^3,3 ^3,4 ^3,5 Napaka pri navajanju: Neveljavna značka <ref>; sklici, imenovani Karttunen2016, ne vsebujejo nobenega besedila

[Whitmell1907-4] Napaka pri navajanju: Neveljavna značka <ref>; sklici, imenovani Whitmell1907, ne vsebujejo nobenega besedila

[sizemagnitude-5] Napaka pri navajanju: Neveljavna značka <ref>; sklici, imenovani sizemagnitude, ne vsebujejo nobenega besedila

[Mag_formula-6] Napaka pri navajanju: Neveljavna značka <ref>; sklici, imenovani Mag_formula, ne vsebujejo nobenega besedila

[Albedo-7] Napaka pri navajanju: Neveljavna značka <ref>; sklici, imenovani Albedo, ne vsebujejo nobenega besedila

[Luciuk2-8] Napaka pri navajanju: Neveljavna značka <ref>; sklici, imenovani Luciuk2, ne vsebujejo nobenega besedila

[Mallama_and_Hilton-9] 9,0 ^9,1 Napaka pri navajanju: Neveljavna značka <ref>; sklici, imenovani Mallama_and_Hilton, ne vsebujejo nobenega besedila

[JPLHorizonsVenus-10] Napaka pri navajanju: Neveljavna značka <ref>; sklici, imenovani JPLHorizonsVenus, ne vsebujejo nobenega besedila

[MPC1985-11] Napaka pri navajanju: Neveljavna značka <ref>; sklici, imenovani MPC1985, ne vsebujejo nobenega besedila

[Lagerkvist-12] 12,0 ^12,1 Napaka pri navajanju: Neveljavna značka <ref>; sklici, imenovani Lagerkvist, ne vsebujejo nobenega besedila

[dymock-13] 13,0 ^13,1 ^13,2 Napaka pri navajanju: Neveljavna značka <ref>; sklici, imenovani dymock, ne vsebujejo nobenega besedila

[JPLdoc-14] Napaka pri navajanju: Neveljavna značka <ref>; sklici, imenovani JPLdoc, ne vsebujejo nobenega besedila

[Bennu-15] Napaka pri navajanju: Neveljavna značka <ref>; sklici, imenovani Bennu, ne vsebujejo nobenega besedila

[Shevchenko2016-16] Napaka pri navajanju: Neveljavna značka <ref>; sklici, imenovani Shevchenko2016, ne vsebujejo nobenega besedila

[lc-17] Napaka pri navajanju: Neveljavna značka <ref>; sklici, imenovani lc, ne vsebujejo nobenega besedila

[MPES-18] Napaka pri navajanju: Neveljavna značka <ref>; sklici, imenovani MPES, ne vsebujejo nobenega besedila

[Meisel1976-19] Napaka pri navajanju: Neveljavna značka <ref>; sklici, imenovani Meisel1976, ne vsebujejo nobenega besedila

[COBS_2011L4-20] Napaka pri navajanju: Neveljavna značka <ref>; sklici, imenovani COBS 2011L4, ne vsebujejo nobenega besedila

[MPC2011L4-21] Napaka pri navajanju: Neveljavna značka <ref>; sklici, imenovani MPC2011L4, ne vsebujejo nobenega besedila

[kidger-22] Napaka pri navajanju: Neveljavna značka <ref>; sklici, imenovani kidger, ne vsebujejo nobenega besedila

[Hughes-23] Napaka pri navajanju: Neveljavna značka <ref>; sklici, imenovani Hughes, ne vsebujejo nobenega besedila

[Yoshida-24] 24,0 ^24,1 ^24,2 Napaka pri navajanju: Neveljavna značka <ref>; sklici, imenovani Yoshida, ne vsebujejo nobenega besedila

[Jewitt-25] 25,0 ^25,1 Napaka pri navajanju: Neveljavna značka <ref>; sklici, imenovani Jewitt, ne vsebujejo nobenega besedila

[JPL_289-26] 26,0 ^26,1 Napaka pri navajanju: Neveljavna značka <ref>; sklici, imenovani JPL_289, ne vsebujejo nobenega besedila

[Lamy2004-27] Napaka pri navajanju: Neveljavna značka <ref>; sklici, imenovani Lamy2004, ne vsebujejo nobenega besedila

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

Absolutni izsev

Vsebina

Umovanje o koeficientu a