Deltoida

Nastanek deltoide. Deltoida je prikazana z rdečo barvo.

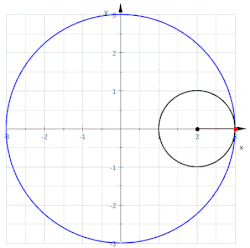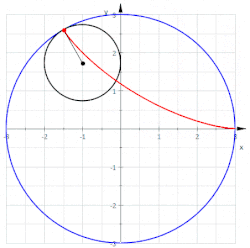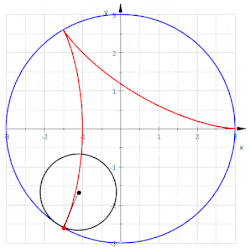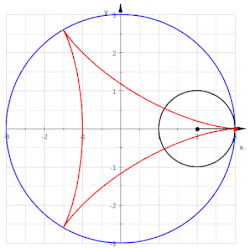
Deltoida (tudi Steinerjeva krivulja in trikuspoida) je hipocikloida, ki ima tri vrhove. Sestavljajo jo trije enaki loki. Spada med hipocikloide. Je tudi ruleta, ki jo naredi točka na obodu krožnice, ko se ta brez drsenja vrti znotraj krožnice, ki ima trikrat večji polmer.

Ime spominja na grško črko delta, ki ji je podobna.

Deltoida v parametričnih koordinatah

V parametričnih koordinatah je enačba deltoide

$x=2a\cos (t)+a\cos (2t)$

$y=2a\sin (t)-a\sin (2t)$

kjer je

• $a$ polmer vrteče se krožnice

V kompleksnih koordinatah je to

$z=2a{e}^{it}+a{e}^{-2it}$.

Deltoida v kartezičnih koordinatah

V kartezičnem koordinatnem sistemu je enačba deltoide

$(x^2+y^2{)}^2+18a^2(x^2+y^2)-27a^4=8a(x^3-3x{y}^2)$.

Krivulja je racionalna, ima geometrijski rod enak 0 in je ravninska algebrska krivulja četrte stopnje.

Krivulja ima tri singularnosti, to so konice, ki odgovarjajo točkam $t=0,\pm \frac{2\pi }{3}$.

Deltoida v polarnih koordinatah

V polarnem koordinatnem sistemu je enačba deltoide

$r^4+18a^2{r}^2-27a^4=8a{r}^3\cos 3\theta$.

Dualna krivulja deltoide

Dualna krivulja deltoide ima enačbo

$x^3-x^2-(3x+1)y^2=0,$

Ploščina in obseg

Ploščina deltoide je enaka

$2\pi a^2$

kjer je

• $a$ polmer vrteče se krožnice

Ploščina deltoide je dvakrat večja kot ploščina vrteče se krožnice.

Obseg (skupna dolžina lokov) deltoide je $16a$ .

Zgodovina

Običajne cikloide sta proučevala že italijanski fizik, matematik, astronom in filozof Galileo Galilei (1564–1642) in francoski matematik, fizik, filozof, teolog, muzikolog in glasbeni teoretik Marin Mersenne (1588-1648). Prvi, ki pa je uporabljal cikloidalne krivulje, je bil danski astronom in matematik Ole Christensen Rømer (1644–1710) v letu 1674 pri proučevanju zobnikov. Švicarski matematik, fizik in astronom Leonhard Euler (1707-1783) je prvi postal pozoren na to krivuljo v letu 1745 v povezavi z optičnimi problemi.

Glej tudi

• seznam krivulj

Zunanje povezave

• Deltoida na Encyclopédie des Formes Mathématiques Remarquables Predloga:Ikona fr
• Deltoida na MacTutor Predloga:Ikona en
• Steinerjeva krivulja Predloga:Ikona en