Fourierova vrsta

Prvi štirje približki Fourierovih vrst za pravokotni val.

Fourierove vrste v matematiki omogočajo razstavljanje poljubne periodične funkcije ali periodičnega signala v vsoto (po možnosti končno) skupine periodičnih funkcij kot sta sinus in kosinus. Proučevanje Fourierovih vrst je veja Fourierove analize.

Tako se lahko na primer funkcijo $S(x)$ razvije v neskončno vrsto po sinusih:

$S(x)=b_1\sin x+b_2\sin 2x+b_3\sin 3x+\cdots =\sum _{n=1}^{\mathrm{\infty }}{b}_n\sin nx.$

Lahko pa se neko drugo funkcijo $C(x)$ razvije v neskončno vrsto po kosinusih:

$C(x)=b_0+b_1\cos x+b_2\cos 2x+b_3\cos 3x+\cdots =b_0+\sum _{n=1}^{\mathrm{\infty }}{b}_n\cos nx.$

Pri tem obe funkciji ohranita nekatere osnovne značilnosti, kot so periodičnost, lihost (ali sodost), vrednost pri $x=0$ in $x=\pi$.

Imenujejo se po francoskem fiziku in matematiku Josephu Fourieru (1768–1830).

Definicija

Fourierov obrazec za periodične funkcije

Naj je periodična funkcija $f(x)$ s periodo $2\pi$, ki je integrabilna na intervalu $[-\pi ,\pi ]$. Števila:

$a_n=\frac{1}{\pi }\underset{-\pi }{\overset{\pi }{\int }}f(x)\cos (nx)\mathrm{d}x,n\ge 0$

in:

$b_n=\frac{1}{\pi }\underset{-\pi }{\overset{\pi }{\int }}f(x)\sin (nx)\mathrm{d}x,n\ge 1$

se imenujejo Fourierovi koeficienti za funkcijo $f(x)$.

Včasih se uporablja tudi Fourierove vrste za $f$, ki se jih označuje z:

$(S_{N}f)(x)=\frac{a_0}{2}+\sum _{n=1}^N[a_n\cos (nx)+b_n\sin (nx)],N\ge 0.$

Delne vsote za $f$ so trigonometrični polinomi. Pričakuje se, da funkcije $S_N$ za $f$ dajejo približek, ki se približuje vrednosti za $f$, ko gre $N$ proti neskončnosti. Neskončna vsota v obliki:

$\frac{a_0}{2}+\sum _{n=1}^{\mathrm{\infty }}[a_n\cos (nx)+b_n\sin (nx)]$

se imenuje Fourierova vrsta za $f$.

Fourierova vrsta ne konvergira vedno, saj se včasih celo za neko vrednost $x_0$ vsota vrste v tej točki razlikuje od vrednosti $f(x_0)$ te funkcije. Harmonična analiza je področje, ki se ukvarja s konvergenco Fourierovih vrst. Kadar je kvadrat funkcije integrabilen na intervalu $[-\pi ,\pi ]$, takrat Fourierova vrsta konvergira skoraj v vsaki točki. Predpostavi se lahko, da Fourierova vrsta konvergira v vsaki točki razen v točkah nezveznosti.

Zgled periodične funkcije, ki se imenuje žagasti val.

Animacija prvih petih zaporednih delnih Fourierovih vrst.

Zgled

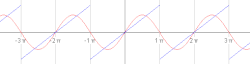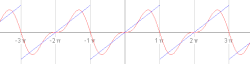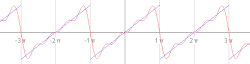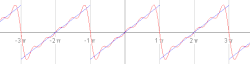
V zgledu se obravnava žagasti val in se ga razvije v Fourierovo vrsto. Žagasti val se opiše z naslednjo funkcijo:

$f(x)=x,\mathrm{z}\mathrm{a}-\pi <x<\pi ,$

$f(x+2\pi )=f(x),\mathrm{z}\mathrm{a}-\mathrm{\infty }<x<\mathrm{\infty }.$

V tem primeru se dobi za Fourierove koeficiente:

$\begin{array}{cc}{a}_0& =\frac{1}{\pi }\underset{-\pi }{\overset{\pi }{\int }}x\mathrm{d}x=0.\\ a_n& =\frac{1}{\pi }\underset{-\pi }{\overset{\pi }{\int }}x\cos (nx)\mathrm{d}x=0,n\ge 0.\\ b_n& =\frac{1}{\pi }\underset{-\pi }{\overset{\pi }{\int }}x\sin (nx)\mathrm{d}x=-\frac{2}{n}\cos (n\pi )+\frac{2}{\pi n^2}\sin (n\pi )=2\frac{(-1{)}^{n+1}}{n},n\ge 1.\end{array}$

Lahko se dokaže, da Fourierova vrsta konvergira k vrednosti $f(x)$ v vsaki točki, kjer je funkcija $f$ diferenciabilna. Torej se lahko zapiše:

$\begin{array}{cc}f(x)& =\frac{a_0}{2}+\sum _{n=1}^{\mathrm{\infty }}[a_n\cos \left(nx\right)+b_n\sin \left(nx\right)]\\ & =2\sum _{n=1}^{\mathrm{\infty }}\frac{(-1{)}^{n+1}}{n}\sin (nx),\mathrm{z}\mathrm{a}x-\pi \notin 2\pi Z.\end{array}$

Eksponentna Fourierova vrsta

Uporabi se Eulerjev obrazec, ki ima obliko:

$e^{inx}=\cos (nx)+i\sin (nx),$

kjer je:

• $i$ – imaginarna enota

S tem se dobi bolj zgoščeno obliko za Fourierovo vrsto:

$f(x)=\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}{c}_n{e}^{inx}.$

Fourierovi koeficienti pa so:

$c_n=\frac{1}{2\pi }\underset{-\pi }{\overset{\pi }{\int }}f(x)e^{-inx}\mathrm{d}x.$

$a_n=c_n+c_{-n}\text{ za }n=0,1,2,\dots$

$b_n=i(c_n-c_{-n})\text{ za }n=1,2,\dots$

in:

$c_n=\{\begin{array}{cc}\frac{1}{2}(a_n-i{b}_n)& n>0\\ \frac{1}{2}{a}_0& n=0\\ \frac{1}{2}(a_{-n}+i{b}_{-n})& n<0\end{array}$

Zelo primerno je uporabiti obliko za $f$ tako, da se dobi obrazec v obliki:

$f(x)=\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}\hat{f}(n)\cdot e^{inx}.$

V tehniki se pogosto uporablja naslednjo obliko:

$f(x)=\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}F[n]\cdot e^{inx},$

kjer:

• $F[n]$ pomeni, da je uporabljena nezvezna domena frekvenc. Zelo pogosto v tehniki spremenljivka $x$ predstavlja čas.

Fourierove vrste v splošnem intervalu

Obravnava se splošni interval $[a,a+\tau ]$, kjer je s periodo $\tau$ za vsa realna števila definirana funkcija $g(x)$ s kompleksnimi koeficienti $G(n)$. Lahko se zapiše:

$g(x)=\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}G[n]\cdot e^{i2\pi \frac{n}{\tau }x}.$

Če je funkcija kvadratno integrabilna (velja: $\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}|f(x){|}^2\mathrm{d}x<\mathrm{\infty }$), v intervalu $[a,a+\tau ]$, se jo lahko v tem intervalu prikaže z zgornjim obrazcem. To pa pomeni, da takrat, ko se dobi koeficiente za funkcijo $h(x)$ z:

$G[n]=\frac{1}{\tau }\underset{a}{\overset{a+\tau }{\int }}h(x)\cdot e^{-i2\pi \frac{n}{\tau }x}\mathrm{d}x,$

potem je $g(x)$ povsod na intervalu $[a,a+\tau ]$ enak $h(x)$. Iz tega sledi, da ima $h(x)$ periodo enako $\tau$ in, da naslednje

• sta $g(x)$ in $h(x)$ povsod enaka, razen na mestih nezveznosti
• $a$ se lahko poljubno izbere. Najpogosteje se izbere $a=0$ in $a=\tau /2$.

Fourierove vrste v kvadratu

Definira se lahko tudi Fourierove vrste za dve spremenljivki x in y v kvadratu $[-\pi ,\pi ]\times [-\pi ,\pi ]$:

$f(x,y)=\sum _{j,k\in \mathbb{Z}}{c}_{j,k}{e}^{ijx}{e}^{iky},$

kjer je:

$c_{j,k}=\frac{1}{4{\pi }^2}\underset{-\pi }{\overset{\pi }{\int }}\underset{-\pi }{\overset{\pi }{\int }}f(x,y)e^{-ijx}{e}^{-iky}\mathrm{d}x\mathrm{d}y.$

Hilbertov prostor

Če se obravnava Hilbertove prostore, množica funkcij $\{e_n=e^{inx},n\in \mathbb{Z}\}$ tvori ortonormalno bazo prostora $L^2([-\pi ,\pi ])$ za kvadratno integrabilne funkcije v $[-\pi ,\pi ]$. Ta prostor je Hilbertov prostor z notranjim produktom za poljubna dva elementa $f$ in $g$, ki je definiran kot:

$⟨f,g⟩\stackrel{\mathrm{d}\mathrm{e}\mathrm{f}}{=}\frac{1}{2\pi }\underset{-\pi }{\overset{\pi }{\int }}f(x)\overline{g(x)}\mathrm{d}x.$

Osnovne Fourierove vrste v Hilbertovih prostorih se lahko zapiše kot:

$f=\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}⟨f,e_n⟩e_n.$

To pa je enakovredno s kompleksno eksponentno obliko (glej zgoraj). Oblika s sinusom in kosinusom tvori ortogonalno množico:

$\underset{-\pi }{\overset{\pi }{\int }}\cos (mx)\cos (nx)\mathrm{d}x=\pi {\delta }_{mn},m,n\ge 1,$

$\underset{-\pi }{\overset{\pi }{\int }}\sin (mx)\sin (nx)\mathrm{d}x=\pi {\delta }_{mn},m,n\ge 1$

$\underset{-\pi }{\overset{\pi }{\int }}\cos (mx)\sin (nx)\mathrm{d}x=0,$

kjer je:

• ${\delta }_{mn}$ – Kroneckerjeva delta.

Značilnosti

Funkcija $f$ pripada $C^k(𝕋)$, če je $f$ funkcija s periodo $2\pi$ nad $ℝ$ in, če je ta k-krat odvedljiva in je k-ti odvod zvezen. Označi se n-ti Fourierov koeficient z $\hat{f}(n)$.

• če je $f$ periodična liha funkcija, potem so $a_n=0$ za vse $n$
• če je $f$ periodična soda funkcija, potem so $b_n=0$ za vse $n$
• če je $f$ integrabilna funkcija velja $\underset{|n|\to \mathrm{\infty }}{\lim }\hat{f}(n)=0$ ter $\underset{n\to +\mathrm{\infty }}{\lim }{a}_n=0$ in $\underset{n\to +\mathrm{\infty }}{\lim }{b}_n=0$. To je Riemann-Lebesguov izrek
• dvojno neskončno zaporedje $\{a_n\}$ v $c_o$ je zaporedje Fourierovih koeficientov funkcije v $L^1[0,2\pi ]$, če in samo če je to konvolucija v ${\ell }^2(\mathbb{Z})$
• Parsevalov izrek: če je $f\in L^2([-\pi ,\pi ])$, potem je tudi $\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}|\hat{f}(n){|}^2=\frac{1}{2\pi }\underset{-\pi }{\overset{\pi }{\int }}|f(x){|}^2\mathrm{d}x$
• Plancherelov izrek: če so $c_0,c_{\pm 1},c_{\pm 2},\dots$ koeficienti in velja $\sum _{n=-\mathrm{\infty }}^{\mathrm{\infty }}|c_n{|}^2<\mathrm{\infty }$, potem obstaja funkcija $f\in L^2([-\pi ,\pi ])$ tako, da velja $\hat{f}(n)=c_n$ za vsak $n$
• prvi konvolucijski izrek pravi, da takrat, ko sta $f$ in $g$ v L¹([−π, π]), potem velja tudi $\widehat{f*g}(n)=2\pi \hat{f}(n)\hat{g}(n)$, kjer je ƒ ∗ g konvolucija s periodo $2\pi$ funkcij $f$ in $g$
• drugi konvolucijski izrek pravi, da je $\widehat{f\cdot g}=\hat{f}*\hat{g}$.

Posplošitve

Obstaja več vrst posplošitev Fourierovih vrst. Njihovo proučevanje se imenuje harmonična analiza.

Približki in konvergenca Fourierovih vrst

Gibbsov pojav

Približek reda 10 za pravokotni val.

Približek reda 50 za pravokotni val.

Približek reda 250 za pravokotni val.

Zelo pomembno vprašanje je povezano s konvergenco Fourierovih vrst. Pogosto je treba zamenjati neskončno vrsto $\sum _{-\mathrm{\infty }}^{\mathrm{\infty }}$ s končno: $(S_{N}f)(x)=\sum _{n=-N}^N\hat{f}(n)e^{inx}$. Takšna vrsta se imenuje delna vsota. Želi se vedeti kako vrednost $(S_{N}f)(x)$ konvergira k $f(x)$, ko gre $N$ proti neskončnosti.

Divergenca Fourierovih vrst

Fourierove vrste so izredno dobro konvergentne. Vrste, ki bi bile divergentne so zelo redke. V letu 1922 je ruski matematik Andrej Nikolajevič Kolmogorov (1903–1987) v enem svojih del podal primer integrabilne funkcije, katere Fourierova vrsta je skoraj povsod divergentna.

Glej tudi

• Laurentova vrsta
• harmonična analiza
• spektralna teorija
• Fourierova transformacija
• Fejérov izrek
• Dichletovo jedro

Zunanje povezave

• Fourierova vrsta Predloga:Webarchive Predloga:Ikona sl
• Fourierova vrsta na e-študij Predloga:Webarchive Predloga:Ikona sl
• Predloga:MathWorld
• Apleti za prikaz Fourierovih vrst Predloga:Ikona en
• Fourierove vrste Predloga:Ikona en
• Učbenik Predloga:Ikona en
• Maths Online Predloga:Ikona en
• Fourierove vrste in Fourierovi integrali Predloga:Ikona en