Epitrohoida

Epotrohoida z R = 3, r = 1 in d = 1/2

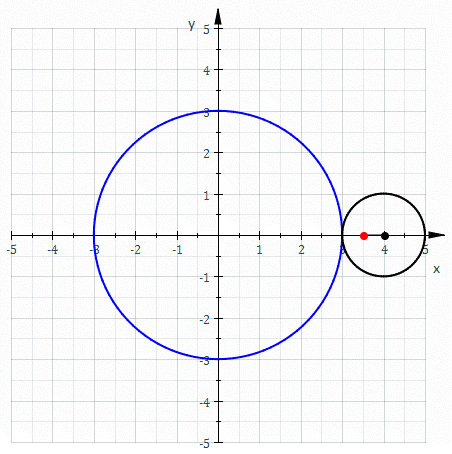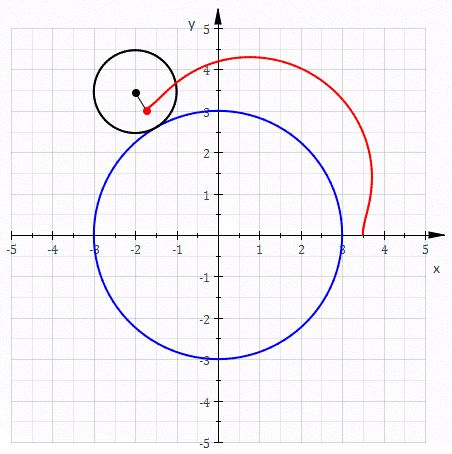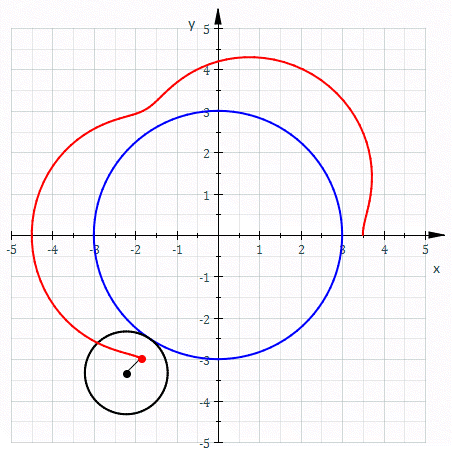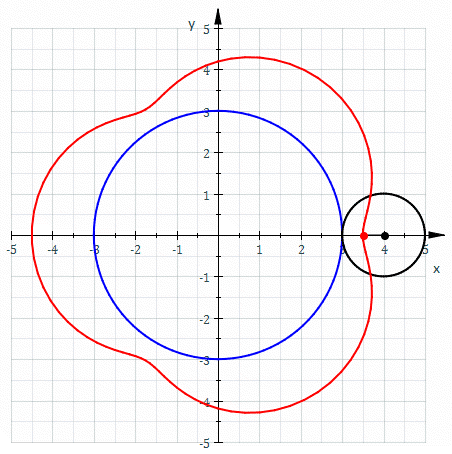
Epitrohoida je krivulja ruleta, ki jo dobimo tako, da sledimo izbrani točki na krožnici s polmerom $r$, ki se brez drsenja kotali po krožnici s polmerom $R$ in $d$ je razdalja izbrane točke od središča krožnice.

Epitrohoida v polarnih koordinatah

V polarnem koordinatnem sistemu je enačba epitrohoide

$r(\theta {)}^2=(R+r{)}^2-2d(R+r)\cos \left(\frac{R}{r}\theta \right)+d^2,$.

Epitrohoida v parametrični obliki

V parametrični obliki je enačba epitrohoide

$x(\theta )=(R+r)\cos \theta -d\cos \left(\frac{R+r}{r}\theta \right),$

$y(\theta )=(R+r)\sin \theta -d\sin \left(\frac{R+r}{r}\theta \right).$

Posebni primeri

Med posebnimi primeri epitrohoide je Pascalov polž z $R=r$ in epicikloida z $d=r$.

Tirnice planetov v starem Ptolomejevem sistemu so bile epitrohoide.

Glej tudi

• cikloida
• epicikloida
• hipocikloida
• hipotrohoida
• seznam krivulj

Zunanje povezave

• Epitrohoida na MathWorld Predloga:Ikona en
• Epitrohoida na Xah Lee Predloga:Ikona en
• Epitrohoida na Mactutor Predloga:Webarchive Predloga:Ikona en
• Krivulje gibanja planetov v geocentričnem sistemu (interaktivna simulacija)