Število praštevil

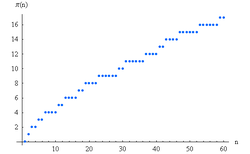
Števílo práštevíl je v matematiki nemultiplikativna aritmetična funkcija poljubnega pozitivnega realnega števila $x$, ki se jo označi s $\pi (x)$, in da število praštevil, ki ne presegajo $x$. Po navadi se namesto realnega števila vzame pozitivno celo število $n$. Prve vrednosti $\pi (n)$ za n = 1, 2, 3, ... so Predloga:OEIS:

0, 1, 2, 2, 3, 3, 4, 4, 4, 4, 5, 5, 6, 6, 6, 7, 7, 8, 8, ...

Graf prvih 60 vrednosti funkcije $\pi (n)$

Zgodovina

V teoriji števil je pomembno raziskovanje obnašanja števila praštevil. Gauss in Legendre sta domnevala, da je vrednost funkcije približno enaka:

$x/\ln x,$

tako da je limita kvocienta funkcij $\pi (x)$ in $x/\ln x$:

$\underset{x\to +\mathrm{\infty }}{\lim }\frac{\pi (x)}{x/\ln x}=1.$

Asimptotično obnašanje $\pi (x)\sim x/\ln x$, je dano s praštevilskim izrekom.

Enakovredno kot zgoraj velja:

$\underset{x\to +\mathrm{\infty }}{\lim }\pi (x)/\mathrm{li}(x)=1,$

kjer je $\mathrm{li}(x)$ fukcija logaritemskega integrala. Praštevilski izrek sta leta 1896 neodvisno dokazala Hadamard in La Vallée Poussin s pomočjo značilnosti Riemannove funkcije ζ, ki jo je uvedel Riemann leta 1859.

Znane so točnejše ocene za $\pi (x)$, kot je na primer:

$\pi (x)=\mathrm{li}(x)+𝒪(x\exp (-\frac{\sqrt{\ln (x)}}{15})),$

kjer je $𝒪$ Landauov simbol. Elementarne dokaze praštevilskega izreka brez uporabe funkcije ζ ali kompleksne analize sta leta 1948 večinoma neodvisno odkrila Selberg in Erdős.

Funkcijo $\pi (x)$ je raziskoval James Joseph Sylvester.

Podobna je domneva za praštevilske vrste:

$G(n,x)=\sum _p^x{p}^n\sim \pi (x^{n+1}).$

Algoritmi za računanje $\pi (x)$

Preprost način za računanje $\pi (x)$, če $x$ ni prevelik, je Eratostenovo sito, s katerim se najde praštevila manjša ali enaka $x$, in se jih prešteje.

Bolj izdelano pot je podal Legendre. Če so za dani $x$ $p_1$, $p_2$, ..., $p_k$ različna praštevila, je število celih števil manjših ali enakih od $x$, ki niso deljiva s $p_i$:

$\lfloor x\rfloor -\sum _i\lfloor \frac{x}{p_i}\rfloor +\sum _{i<j}\lfloor \frac{x}{p_i{p}_j}\rfloor -\sum _{i<j<k}\lfloor \frac{x}{p_i{p}_j{p}_k}\rfloor +\cdots ,$

kjer je $\lfloor \cdot \rfloor$ funkcija celega dela. To število je tako enako:

$\pi (x)-\pi \left(\sqrt{x}\right)+1,$

kjer so števila $p_1,p_2,\dots ,p_k$ praštevila manjša ali enaka kvadratnemu korenu od $x$.

Meissel je v nizu člankov, objavljenih med letoma 1870 in 1885, opisal in uporabil praktični kombinatorični način računanja $\pi (x)$. Naj bodo $p_1$, $p_2$, ..., $p_n$ prva $n$ praštevila in naj $\mathrm{\Phi }(m,n)$ označuje število naravnih števil manjših od $m$, ki niso deljiva s kakšnim $p_i$. Potem velja:

$\mathrm{\Phi }(m,n)=\mathrm{\Phi }(m,n-1)-\mathrm{\Phi }(\left[\frac{m}{p_n}\right],n-1).$

Če za dano naravno število $m$ velja $n=\pi \left(\sqrt[3]{m}\right)$ in $\mu =\pi \left(\sqrt{m}\right)-n$, potem velja:

$\pi (m)=\mathrm{\Phi }(m,n)+n(\mu +1)+\frac{{\mu }^2-\mu }{2}-1-\sum _{k=1}^{\mu }\pi \left(\frac{m}{p_{n+k}}\right).$

S tem pristopom je Meissel izračunal $\pi (x)$ za $x$ enak 5 · 10⁵, 10⁶, 10⁷ in 10⁸.

Leta 1959 je Lehmer razširil in poenostavil Meisslovo metodo. Za realno število $m$ in za naravni števili $n$ in $k$ naj je $P_k(m,n)$ število števil manjših od $m$ z natanko $k$ prafaktorji, večjimi od $p_n$. Naj velja tudi $P_0(m,n)=1$. Potem je:

$\mathrm{\Phi }(m,n)=\sum _{k=0}^{+\mathrm{\infty }}{P}_k(m,n),$

kjer ima vsota dejansko le končno število neničelnih členov. Naj $y$ označuje takšno celo število, da je $\sqrt[3]{m}\le y\le \sqrt{m}$ in naj je $n=\pi (y)$. Potem je $P_1(m,n)=\pi (m)-n$ in $P_k(m,n)=0$, ko je $k\ge 3$. Zato:

$\pi (m)=\mathrm{\Phi }(m,n)+n-1-P_2(m,n).$

$P_2(m,n)$ je moč izračunati kot:

$P_2(m,n)=\sum _{y<p\le \sqrt{m}}(\pi \left(\frac{m}{p}\right)-\pi (p)+1).$

$\mathrm{\Phi }(m,n)$ se lahko izračuna s pomočjo naslednjih pravil:

1. $\mathrm{\Phi }(m,0)=\lfloor m\rfloor ,$
2. $\mathrm{\Phi }(m,b)=\mathrm{\Phi }(m,b-1)-\mathrm{\Phi }(\frac{m}{p_b},b-1).$

S pomočjo te metode in računalnika IBM 701 je Lehmer lahko izračunal $\pi \left(10^{10}\right)$.

Hvang Čeng je na konferenci o praštevilih na Univerzi v Bordeauxu uporabil naslednji enakosti:

$e^{(a-1)\mathrm{\Theta }}f(x)=f(ax),$

$J(x)=\sum _{n=1}^{\mathrm{\infty }}\frac{\pi (x^{1/n})}{n},$

pri čemer je $x=e^t$. Z Laplaceovo transformacijo obeh strani in geometrično vsoto $e^{n\mathrm{\Theta }}$ izhaja:

$\frac{1}{2\pi i}\underset{c-i\mathrm{\infty }}{\overset{c+i\mathrm{\infty }}{\int }}g(s)t^s\mathrm{d}s=\pi (t),$

$\frac{\ln \zeta (s)}{s}=(1-e^{\mathrm{\Theta }(s)}{)}^{-1}g(s),$

$\mathrm{\Theta }(s)=s\frac{\mathrm{d}}{\mathrm{d}s}.$

Druge funkcije štetja praštevil

Uporabljajo se tudi druge funkcije, ker je lažje delati z njimi. Ena od njih je Riemannova funkcija števila praštevil, običajno označena kot ${\mathrm{\Pi }}_0(x)$ in tudi $f(x)$. Funkcija narašča korakoma po $1/n$ za praštevilske potence $p^n$, in zavzema vrednosti na polovici obeh nezveznosti. Na ta način je lahko določena z obratom Mellinove transformacije. Strogo se lahko določi ${\mathrm{\Pi }}_0(x)$ kot:

${\mathrm{\Pi }}_0(x)=\frac{1}{2}(\sum _{p^n<x}\frac{1}{n}+\sum _{p^n\le x}\frac{1}{n}),$

kjer je $p$ praštevilo.

Lahko se piše tudi:

${\mathrm{\Pi }}_0(x)=\sum _2^x\frac{\mathrm{\Lambda }(n)}{\ln n}-\frac{1}{2}\frac{\mathrm{\Lambda }(x)}{\ln x}=\sum _{n=1}^{\mathrm{\infty }}\frac{1}{n}{\pi }_0(x^{1/n}),$

kjer je $\mathrm{\Lambda }(n)$ von Mangoldtova funkcija in:

${\pi }_0(x)=\frac{\pi (x-0)+\pi (x+0)}{2}.$

Möbiusova inverzna formula da:

${\pi }_0(x)=\sum _{n=1}^{\mathrm{\infty }}\frac{\mu (n)}{n}{\mathrm{\Pi }}_0(x^{1/n})=\underset{1}{\overset{\mathrm{\infty }}{\int }}du{M}^{\prime }(u){\mathrm{\Pi }}_0(x^{1/u})u^{-1},$

kjer je $M(u)$ Mertensova funkcija.

Z zvezo med Riemannovo funkcijo ζ(·) in von Mangoldtovo funkcijo Λ(·) ter Perronovo enačbo je:

$\ln \zeta (s)=s\underset{0}{\overset{\mathrm{\infty }}{\int }}{\mathrm{\Pi }}_0(x)x^{-s+1}dx.$

Funkcija $\pi (x)$ je v tesni zvezi s funkcijama Čebišova θ(x) in ψ(x), ki razvrščata praštevila ali praštevilske potence $p^n$ z $\ln p$:

$\theta (x)=\sum _{p\le x}\ln p,$

$\psi (x)=\sum _{p^n\le x}\ln p=\sum _{n=1}^{\mathrm{\infty }}\theta (x^{1/n})=\sum _{n\le x}\mathrm{\Lambda }(n).$