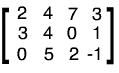Linearna algebra

Nekateri predmeti, ki jih proučuje linearna algebra Vektor V tridimenzionalnem evklidskem prostoru te tri ravnine predstavljajo rešitve linearnih enačb, njihov presek pa skupek skupnih rešitev: v tem primeru ena točka. Modra črta je skupna rešitev dveh enačb. Linearne transformacije Sistemi linearnih enačb Matrike $𝐀\xi =\lambda \xi$ Lastne vrednosti in lastni vektorji Kvadriki Tenzorji

Linearna algebra je matematična disciplina, ki se ukvarja s proučevanjem vektorjev, vektorskih prostorov (ali linearnih prostorov), linearnih transformacij in sistemov linearnih enačb. Konkretno upodobitev linearne algebre najdemo v analitični geometriji. Vektorski prostori so osrednja tema sodobne matematike; torej se linearna algebra na široko uporablja v abstraktni algebri in funkcionalni analizi. Zelo je uporabna tudi v naravoslovnih in družboslovnih znanostih.

Nanaša na linearne enačbe, kot so:

$a_1{x}_1+\cdots +a_n{x}_n=b,$

linearne transformacije, kot so:

$(x_1,\dots ,x_n)\mapsto a_1{x}_1+\cdots +a_n{x}_n,$

in njihove predstavitve v vektorskih prostorih in skozi matrice.

Linearna algebra je osnova za skoraj vsa področja matematike. Na primer, linearna algebra je temeljna v sodobnih predstavitvah geometrije, vključno z definicijami osnovnih objektov, kot so črte, ravnine in rotacije. Tudi funkcionalno analizo, vejo matematične analize, lahko razumemo kot aplikacijo linearne algebre v prostorih funkcij.

Linearna algebra se uporablja tudi v velikem številu znanostih in področij tehnike, saj omogoča modeliranje številnih naravnih pojavov in učinkovito računanje s takšnimi modeli. Za nelinearne sisteme, ki jih ni mogoče modelirati z linearno algebro, se pogosto uporabljajo približki prvega reda.

Vektorski prostori

Predloga:Glavni Do 19. stoletja je bila linearna algebra predstavljena s sistemi linearnih enačb in matrik. V sodobni matematiki se na splošno prednostno uporablja z vektorskimi prostori, ker je bolj aksiomatična, bolj splošna (ni omejena na končnorazsežne primere) in konceptualno enostavnejša, čeprav bolj abstraktna.

Vektorski prostor nad poljem Predloga:Matematična formula (pogosto polje realnih števil) je množica Predloga:Matematična formula opremljena z dvema binarnima operacijama, ki izpolnjujeta sledeče aksiome. Elementi Predloga:Matematična formula se imenujejo vektorji, elementi F pa skalarji. Prva operacija, seštevanje vektorjev, vzame katera koli dva vektorja Predloga:Matematična formula in Predloga:Matematična formula in rezultat je tretji vektor Predloga:Matematična formula. Druga operacija, skalarno množenje, vzame kateri koli skalar Predloga:Matematična formula in kateri koli vektor Predloga:Matematična formula in rezultat je nov Predloga:Brez preloma. Aksiomi, ki jih morata zadovoljiti seštevanje in skalarno množenje, so navedeni spodaj. (Na spodnjem seznamu so Predloga:Matematična formula in Predloga:Matematična formula poljubni elementi Predloga:Matematična formula, Predloga:Matematična formula in Predloga:Matematična formula sta poljubna skalarja v polju Predloga:Matematična formula)

Aksiom	Označevanje
Asociativnost seštevanja	Predloga:Matematična formula
Komutativnost seštevanja	Predloga:Matematična formula
Identiteta seštevanja	Obstaja element Predloga:Matematična formula znotraj Predloga:Matematična formula, imenovan ničelni vektor (ali preprosto nič), tako da Predloga:Matematična formula za vse Predloga:Matematična formula znotraj Predloga:Matematična formula
Inverzni elementi seštevanja	Za vsak Predloga:Matematična formula znotraj Predloga:Matematična formula obstaja element Predloga:Matematična formula znotraj Predloga:Matematična formula, imenovan nasprotna vrednost od Predloga:Matematična formula, tako da je Predloga:Matematična formula
Distributivnost skalarnega množenja glede na vektorsko seštevanje	Predloga:Matematična formula
Distributivnost skalarnega množenja glede na seštevanje polj	Predloga:Matematična formula
Združljivost skalarnega množenja z množenjem polja	Predloga:Matematična formula Predloga:Efn
Identiteta skalarnega množenja	Predloga:Matematična formula, kjer Predloga:Matematična formula označuje multiplikativno identiteto Predloga:Mvar

Prvi štirje aksiomi pomenijo, da je Predloga:Matematična formula abelova grupa pri seštevanju.

Element določenega vektorskega prostora ima lahko različno naravo; lahko je na primer zaporedje, funkcija, polinom ali matrika. Linearna algebra se ukvarja s tistimi lastnostmi objektov, ki so skupni vsem vektorskim prostorom.

Linearne preslikave

Predloga:Glavni Linearne preslikave so preslikave med vektorskimi prostori, ki ohranjajo strukturo vektorskega prostora. Če obstajata dva vektorska prostora Predloga:Matematična formula in Predloga:Matematična formula nad poljem Predloga:Mvar, potem je linearna preslikava (v nekaterih kontekstih imenovana tudi linearna transformacija) preslikava

$T:V\to W$

to je združljivo z seštevanjem in skalarnim množenjem, tj.

$T(𝐮+𝐯)=T(𝐮)+T(𝐯),T(a𝐯)=aT(𝐯)$

za vse vektorje Predloga:Matematična formula znotraj Predloga:Matematična formula in skalar Predloga:Math znotraj Predloga:Mvar

To pomeni, da za katerikoli vektorje Predloga:Math znotraj Predloga:Math in skalarje Predloga:Math znotraj Predloga:Mvar, ima eden

$T(a𝐮+b𝐯)=T(a𝐮)+T(b𝐯)=aT(𝐮)+bT(𝐯)$

Kadar sta Predloga:Matematična formula isti vektorski prostor, je linearna preslikava $T:V\to V$ znan tudi kot linearni operator na Predloga:Mvar

Bijektivna linearna preslikava med dvema vektorskima prostoroma (torej je vsak vektor iz drugega prostora povezan z natanko enim v prvem) je izomorfizem. Ker izomorfizem ohranja linearno strukturo, sta dva izomorfna vektorska prostora "v bistvu enaka" z vidika linearne algebre, v smislu, da ju z lastnostmi vektorskega prostora ni mogoče razlikovati. Bistveno vprašanje linearne algebre je preizkusiti, ali je linearna preslikava izomorfizem ali ne, in če ni izomorfizem, najti njegovo sliko in niz elementov, ki se preslikajo v ničelni vektor, imenovano jedro preslikave. Vsa ta vprašanja je mogoče rešiti z Gaussovo eliminacijo ali kakšno različico tega algoritma.

Podprostori, linearna ogrinjača in baze

Predloga:Glavni  Proučevanje tistih podskupin vektorskih prostorov, ki so sami po sebi vektorski prostori pri induciranih operacijah, je temeljno, podobno kot pri mnogih matematičnih strukturah. Te podskupine imenujemo linearni podprostori. Natančneje, linearni podprostor vektorskega prostora Predloga:Mvar nad poljem Predloga:Mvar je podmnožica Predloga:Mvar od Predloga:Mvar, tako da sta Predloga:Math in Predloga:Math v Predloga:Mvar za vsak Predloga:Math, Predloga:Math znotraj Predloga:Mvar in vsak Predloga:Mvar znotraj Predloga:Mvar. (Ti pogoji zadoščajo, da je Predloga:Mvar vektorski prostor.)

Na primer, glede na linearno preslikavo $T:V\to W$, slika Predloga:Matematična formula od Predloga:Mvar in inverzna slika Predloga:Matematična formula od 0 (imenovana jedro ali ničelni prostor) sta linearna podprostora od Predloga:Mvar in Predloga:Mvar

Drug pomemben način oblikovanja podprostora je obravnava linearnih kombinacij množice Predloga:Mvar vektorjev: množice vseh vsot

$a_1{𝐯}_1+a_2{𝐯}_2+\cdots +a_k{𝐯}_k,$

kjer Predloga:Matematična formula v Predloga:Mvar in Predloga:Matematična formula v Predloga:Mvar tvorijo linearni podprostor, imenovan ogrinjača Predloga:Mvar Ogrinjača Predloga:Mvar je tudi presečišče vseh linearnih podprostorov, ki vsebujejo Predloga:Mvar Z drugimi besedami, to je najmanjši (za vključitveno razmerje) linearni podprostor, ki vsebuje Predloga:Mvar

Množica vektorjev je linearno neodvisna, če noben ni v ogrinjači drugih. Enako je množica Predloga:Mvar vektorjev linearno neodvisna, če je edini način za izražanje ničelnega vektorja kot linearne kombinacije elementov Predloga:Mvar vzemanje ničle za vsak koeficient $a_i.$

Niz vektorjev, ki obsega vektorski prostor, se imenuje linearna ogrinjača ali generator množic. Če je linearna ogrinjača Predloga:Mvar linearno odvisen, potem je nek element Predloga:Math od Predloga:Mvar v ogrinjači drugih elementov od Predloga:Mvar, in ogrinjača ostane enaka, če odstranimo Predloga:Math iz Predloga:Mvar. Z odstranjevanjem elementov Predloga:Mvar lahko nadaljujemo, dokler ne dobimo linearno neodvisne linearne ogrinjače. Taka linearno neodvisna množica, ki obsega vektorski prostor Predloga:Mvar, se imenuje baza Predloga:Math. Če je Predloga:Mvar linearno neodvisna množica in je Predloga:Mvar linearna ogrinjača, tako da $S\subseteq T,$ potem je baza Predloga:Mvar takšna, da$S\subseteq B\subseteq T.$

Kateri koli dve bazi vektorskega prostora Predloga:Matematična formula imata enako kardinalnost, ki se imenuje dimenzija Predloga:Matematična formula; to je dimenzijski izrek za vektorske prostore. Poleg tega sta dva vektorska prostora nad istim poljem Predloga:Mvar izomorfna izključno takrat, ko imata enako dimenzijo.

Če ima katera koli baza Predloga:Matematična formula (in zato vsaka baza) končno število elementov, je Predloga:Matematična formula končnorazsežni vektorski prostor. Če je Predloga:Matematična formula podprostor od Predloga:Matematična formula, potem je Predloga:Matematična formula V primeru, ko je Predloga:Matematična formula končnorazsežni, enakosti dimenzij implicira Predloga:Matematična formula

Če sta U₁ in U₂ podprostora od V, potem

$\dim (U_1+U_2)=\dim U_1+\dim U_2-\dim (U_1\cap U_2),$

Matrike

Predloga:Glavni  Matrike omogočajo eksplicitno manipulacijo s končnorazsežnimi vektorskimi prostori in linearnimi transformacijami. Njihova teorija je tako bistven del linearne algebre.

Naj bo Predloga:Mvar končnrazsežnini vektorski prostor nad poljem Predloga:Matematična formula , in Predloga:Matematična formula je baza Predloga:Matematična formula (torej je Predloga:Mvar dimenzija Predloga:Matematična formula). Po definiciji baze je transformacija

$\begin{array}{cc}(a_1,\dots ,a_m)& \mapsto a_1{𝐯}_1+\cdots a_m{𝐯}_m\\ F^m& \to V\end{array}$

je bijekcija iz $F^m,$ množica zaporedij Predloga:Mvar elementov od Predloga:Mvar na Predloga:Mvar To je izomorfizem vektorskih prostorov, če ima $F^m$ svojo standardno strukturo vektorskega prostora, kjer se vektorsko seštevanje in skalarno množenje izvajata po komponentah.

Ta izomorfizem omogoča predstavljanje vektorja z njegovo inverzno podobo pod tem izomorfizmom, to je s koordinatami vektorjev $(a_1,\dots ,a_m)$ ali po stolpcu matrike.

$\left[\begin{array}{c}{a}_1\\ ⋮\\ a_m\end{array}\right].$

Če je Predloga:Mvar še en končnorazsežni vektorski prostor (po možnosti enak) z bazo $({𝐰}_1,\dots ,{𝐰}_n),$ linearno transformacijo Predloga:Mvar od Predloga:Mvar do Predloga:Mvar je dobro opredeljen z vrednostmi na baznih elementih, tj $(f({𝐰}_1),\dots ,f({𝐰}_n)).$ Tako je Predloga:Mvar dobro predstavljen s seznamom ustreznih stolpcev matrike. Se pravi, če

$f(w_j)=a_{1,j}{v}_1+\cdots +a_{m,j}{v}_m,$

za Predloga:Matematična formula, potem je Predloga:Mvar predstavljeno z matriko

$\left[\begin{array}{ccc}{a}_{1,1}& \cdots & a_{1,n}\\ ⋮& \ddots & ⋮\\ a_{m,1}& \cdots & a_{m,n}\end{array}\right],$

z Predloga:Mvar vrsticami in Predloga:Mvar stolpci.

Linearni sistemi

Predloga:Glavni  Končna množica linearnih enačb v končni množici spremenljivk, na primer: $x_1,x_2,\dots ,x_n$ ali $x,y,\dots ,z$ se imenuje sistem linearnih enačb ali linearni sistem.

Sistemi linearnih enačb so temeljni del linearne algebre. V preteklosti so se za reševanje takih sistemov uporabljale linearna algebra in teorija matrik. V sodobni predstavitvi linearne algebre s pomočjo vektorskih prostorov in matrik je mogoče številne probleme razložiti z linearnimi sistemi.

Na primer, naj boPredloga:NumBlkPredloga:NumBlklinearni sistem.

Takšnemu sistemu se lahko poveže njegova matrika

$M=\left[\begin{array}{ccc}2& 1& -1\\ -3& -1& 2\\ -2& 1& 2\end{array}\right].$

in njegov desni vektor

$𝐯=\left[\begin{array}{c}8\\ -11\\ -3\end{array}\right].$

Naj bo Predloga:Mvar linearna transformacija povezana z matriko Predloga:Mvar Rešitev sistema (Predloga:EquationNote) je vektor

$𝐗=\left[\begin{array}{c}x\\ y\\ z\end{array}\right]$

tako, da je

$T(𝐗)=𝐯,$

ki je element predslika od v z Predloga:Mvar

Naj bo (Predloga:EquationNote) pridruženi homogeni sistem, kjer so desne strani enačb postavljene na nič:Predloga:NumBlkPredloga:NumBlkRešitve (Predloga:EquationNote) so elementi jedra Predloga:Mvar ali, enako, Predloga:Mvar

Gaussova eleminacija je sestavljena iz izvajanja elementarnih vrstičnih operacij na razširjeni matriki

$\left[\begin{array}{cc}M& 𝐯\end{array}\right]=\left[\begin{array}{cccc}2& 1& -1& 8\\ -3& -1& 2& -11\\ -2& 1& 2& -3\end{array}\right]$

za postavitev v vrstični kanonični formi. Te vrstične operacije ne spremenijo nabora rešitev sistema enačb. V zgledu, vrstična kanonična forma

$\left[\begin{array}{cc}M& 𝐯\end{array}\right]=\left[\begin{array}{cccc}1& 0& 0& 2\\ 0& 1& 0& 3\\ 0& 0& 1& -1\end{array}\right],$

prikazuje, da ima sistem (Predloga:EquationNote) eno rešitev

$\begin{array}{cc}x& =2\\ y& =3\\ z& =-1.\end{array}$

Iz te matrične interpretacije linearnih sistemov izhaja, da se iste metode lahko uporabijo za reševanje linearnih sistemov in za številne operacije na matrikah in linearnih transformacijah, ki vključujejo izračun rangov, jeder, obrnljive matrike.

Glej tudi

• Linearna ogrinjača
• Linearna regresija, statistična metoda ocenjevanja
• Numerična linearna algebra
• Linearno programiranje
• Matrika preslikave

Viri

• Predloga:Citation
• Predloga:Citation
• Predloga:Citation
• Predloga:Citation
• Predloga:Citation
• Predloga:Citation
• Predloga:Citation
• Predloga:Citation
• Predloga:Citation

Zunanje povezave

Spletni viri

• Video predavanja linearne algebre MIT, serija 34 posnetih predavanj profesorja Gilberta Stranga (pomlad 2010)
• Mednarodno društvo linearne algebre
• Predloga:SpringerEOM
• Linearna algebra na MathWorld
• Matrix and Linear Algebra Terms on Earliest Known Uses of Some of the Words of Mathematics
• Earliest Uses of Symbols for Matrices and Vectors on Earliest Uses of Various Mathematical Symbols
• Bistvo linearne algebre, video predstavitev 3Blue1Brown o osnovah linearne algebre s poudarkom na razmerju med geometrijskim, matričnim in abstraktnim stališčem

Spletne knjige

• Predloga:Navedi knjigo
• Predloga:Navedi knjigo9781616100049
• Predloga:Navedi knjigo
•  Predloga:Hefferon Linear Algebra
• Predloga:Navedi knjigo
• Predloga:Navedi knjigo
• Sharipov, Ruslan, Tečaj linearne algebre in večdimenzionalne geometrije
• Treil, Sergei, Linear Algebra Done Wrong